P versus NP problem

Diagram of complexity classes provided that P ≠ NP. The existence of problems outside both P and NP-complete in this case was established by Ladner's theorem.

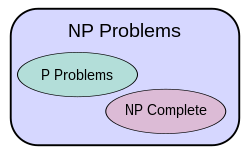
The P versus NP problem is a major unsolved problem in computer science. Informally, it asks whether every problem whose solution can be efficiently checked by a computer can also be efficiently solved by a computer. It was introduced in 1971 by Stephen Cook in his paper "The complexity of theorem proving procedures" and is considered by many to be the most important problem in the field.

In essence, the question P = NP? asks:

Suppose that solutions to a problem can be verified quickly. Then, can the solutions themselves also be computed quickly?

The theoretical notion of quick used here is that of an algorithm that runs in polynomial time. The general class of questions for which some algorithm can provide an answer in polynomial time is called "class P" or just "P".

For some questions, there is no known way to find an answer quickly, but if one is provided with information showing what the answer is, it may be possible to verify the answer quickly. The class questions for which an answer can be verified in polynomial time is called NP.

Consider the subset sum problem, an example of a problem which is easy to verify but whose answer is suspected to be theoretically difficult to compute. Given a set of integers, does some nonempty subset of them sum to 0? For instance, does a subset of the set {−2, −3, 15, 14, 7, −10} add up to 0? The answer "yes, because {−2, −3, −10, 15} add up to zero" can be quickly verified with three additions. However, finding such a subset in the first place could take more time, hence this problem is in NP.

An answer to the P = NP question would determine whether problems like the subset-sum problem that can be verified in polynomial time can also be solved in polynomial time. If it turned out that P does not equal NP, it would mean that some NP problems are harder to compute than to verify: they could not be solved in polynomial time, but the answer could be verified in polynomial time.

Context of the problem

The relation between the complexity classes P and NP is studied in computational complexity theory, the part of the theory of computation dealing with the resources required during computation to solve a given problem. The most common resources are time (how many steps it takes to solve a problem) and space (how much memory it takes to solve a problem).

In such analysis, a model of the computer for which time must be analyzed is required. Typically such models assume that the computer is deterministic (given the computer's present state and any inputs, there is only one possible action that the computer might take) and sequential (it performs actions one after the other).

In this theory, the class P consists of all those decision problems (defined below) that can be solved on a deterministic sequential machine in an amount of time that is polynomial in the size of the input; the class NP consists of all those decision problems whose positive solutions can be verified in polynomial time given the right information, or equivalently, whose solution can be found in polynomial time on a non-deterministic machine. Arguably the biggest open question in theoretical computer science concerns the relationship between those two classes:

Is P equal to NP?

In a 2002 poll of 100 researchers, 61 believed the answer to be no, 9 believed the answer is yes, and 22 were unsure; 8 believed the question may be independent of the currently accepted axioms and so impossible to prove or disprove.

Example

Let ${\mathit {COMPOSITE}}=\{x\in N:x=pq\;{\text{for integers}}\;p,q>1\}$ and $R=\{(x,y)\in N\times N:1<y\leq {\sqrt {x}}\;;\;y\;{\text{divides}}\;x\}.$

Clearly, the question of whether a given $x$ is a composite is equivalent to the question of whether $x$ is a member of ${\mathit {COMPOSITE}}$. It can be shown that ${\mathit {COMPOSITE}}\in \mathbf {NP}$ by verifying that ${\mathit {COMPOSITE}}$ satisfies the above definition.

${\mathit {COMPOSITE}}$ also happens to be in P.

NP-complete

Euler diagram for P, NP, NP-complete, and NP-hard set of problems

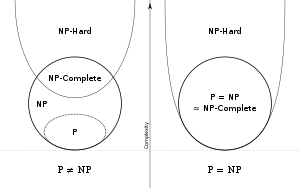
To attack the P = NP question the concept of NP-completeness is very useful. Informally the NP-complete problems are the "toughest" problems in NP in the sense that they are the ones most likely not to be in P. NP-complete problems are a set of problems which any other NP-problem can be reduced to in polynomial time, but which retain the ability to have their solution verified in polynomial time. In comparison, NP-hard problems are those which are at least as hard as NP-complete problems, meaning all NP-problems can be reduced to them, but not all NP-hard problems are in NP, meaning not all of them have solutions which can be verified in polynomial time.

For instance, the decision problem version of the travelling salesman problem is NP-complete, so any instance of any problem in NP can be transformed mechanically into an instance of the traveling salesman problem, in polynomial time. The traveling salesman problem is one of many such NP-complete problems. If any NP-complete problem is in P, then it would follow that P = NP. Unfortunately, many important problems have been shown to be NP-complete, and as of 2010 not a single fast algorithm for any of them is known.

Based on the definition alone it's not obvious that NP-complete problems exist. A trivial and contrived NP-complete problem can be formulated as: given a description of a Turing machine M guaranteed to halt in polynomial time, does there exist a polynomial-size input that M will accept? It is in NP because (given an input) it is simple to check whether or not M accepts the input by simulating M; it is NP-complete because the verifier for any particular instance of a problem in NP can be encoded as a polynomial-time machine M that takes the solution to be verified as input. Then the question of whether the instance is a yes or no instance is determined by whether a valid input exists.

The first natural problem proven to be NP-complete was the Boolean satisfiability problem. This result came to be known as Cook–Levin theorem; its proof that satisfiability is NP-complete contains technical details about Turing machines as they relate to the definition of NP. However, after this problem was proved to be NP-complete, proof by reduction provided a simpler way to show that many other problems are in this class. Thus, a vast class of seemingly unrelated problems are all reducible to one another, and are in a sense "the same problem".

Still harder problems

See also: Complexity class

Although it is unknown whether P = NP, problems outside of P are known. A number of succinct problems (problems which operate not on normal input but on a computational description of the input) are known to be EXPTIME-complete. Because it can be shown that P $\subsetneq$ EXPTIME, these problems are outside P, and so require more than polynomial time. In fact, by the time hierarchy theorem, they cannot be solved in significantly less than exponential time. Examples include finding a perfect strategy for chess (on an N×N board) and some other board games.

The problem of deciding the truth of a statement in Presburger arithmetic requires even more time. Fischer and Rabin proved in 1974 that every algorithm which decides the truth of Presburger statements has a runtime of at least $2^{2^{cn}}$ for some constant c. Here, n is the length of the Presburger statement. Hence, the problem is known to need more than exponential run time. Even more difficult are the undecidable problems, such as the halting problem. They cannot be completely solved by any algorithm, in the sense that for any particular algorithm there is at least one input for which that algorithm will not produce the right answer; it will either produce the wrong answer, finish without giving a conclusive answer, or otherwise run forever without producing any answer at all.

Does P mean "easy"?

The graph shows time (average of 100 instances in msec using a 933 MHz Pentium III) vs.problem size for knapsack problems for a state-of-the-art specialized algorithm. Quadratic fit suggests that empirical algorithmic complexity for instances with 50–10,000 variables is O((log n)²).

All of the above discussion has assumed that P means "easy" and "not in P" means "hard". This assumption, known as Cobham's thesis, though a common and reasonably accurate assumption in complexity theory, is not always true in practice; the size of constant factors or exponents may have practical importance, or there may be solutions that work for situations encountered in practice despite having poor worst-case performance in theory (this is the case for instance for the simplex algorithm in linear programming). Other solutions violate the Turing machine model on which P and NP are defined by introducing concepts like randomness and quantum computation.

Because of these factors, even if a problem is shown to be NP-complete, and even if P ≠ NP, there may still be effective approaches to tackling the problem in practice. There are algorithms for many NP-complete problems, such as the knapsack problem, the travelling salesman problem and the boolean satisfiability problem, that can solve to optimality many real-world instances in reasonable time. The empirical average complexity (time vs. problem size) of such algorithms can be surprisingly low.

Reasons to believe P ≠ NP

According to a poll many computer scientists believe that P ≠ NP. A key reason for this belief is that after decades of studying these problems no one has been able to find a polynomial-time algorithm for any of more than 3000 important known NP-complete problems (see List of NP-complete problems). These algorithms were sought long before the concept of NP-completeness was even defined (Karp's 21 NP-complete problems, among the first found, were all well-known existing problems at the time they were shown to be NP-complete). Furthermore, the result P = NP would imply many other startling results that are currently believed to be false, such as NP = co-NP and P = PH.

It is also intuitively argued that the existence of problems that are hard to solve but for which the solutions are easy to verify matches real-world experience.

If P = NP, then the world would be a profoundly different place than we usually assume it to be. There would be no special value in “creative leaps,” no fundamental gap between solving a problem and recognizing the solution once it’s found. Everyone who could appreciate a symphony would be Mozart; everyone who could follow a step-by-step argument would be Gauss...

— Scott Aaronson, MIT

On the other hand, some researchers believe that we are overconfident in P ≠ NP and should explore proofs of P = NP as well. For example, in 2002 these statements were made:

The main argument in favor of P ≠ NP is the total lack of fundamental progress in the area of exhaustive search. This is, in my opinion, a very weak argument. The space of algorithms is very large and we are only at the beginning of its exploration. [. . .] The resolution of Fermat's Last Theorem also shows that very simple questions may be settled only by very deep theories.

— Moshe Y. Vardi, Rice University

Being attached to a speculation is not a good guide to research planning. One should always try both directions of every problem. Prejudice has caused famous mathematicians to fail to solve famous problems whose solution was opposite to their expectations, even though they had developed all the methods required.

— Anil Nerode, Cornell University

Consequences of proof

One of the reasons the problem attracts so much attention is the consequences of the answer. A proof that P = NP could have stunning practical consequences, if the proof leads to efficient methods for solving some of the important problems in NP. It is also possible that a proof would not lead directly to efficient methods, perhaps if the proof is non-constructive, or the size of the bounding polynomial is too big to be efficient in practice. The consequences, both positive and negative, arise since various NP-complete problems are fundamental in many fields.

Cryptography, for example, relies on certain problems being difficult. A constructive and efficient solution to the NP-complete problem 3-SAT would break many existing cryptosystems such as Public-key cryptography, used for economic transactions over the internet, and Triple DES, used for transactions between banks. These would need to be modified or replaced.

On the other hand, there are enormous positive consequences that would follow from rendering tractable many currently mathematically intractable problems. For instance, many problems in operations research are NP-complete, such as some types of integer programming, and the travelling salesman problem, to name two of the most famous examples. Efficient solutions to these problems would have enormous implications for logistics. Many other important problems, such as some problems in protein structure prediction are also NP-complete; if these problems were efficiently solvable it could spur considerable advances in biology.

But such changes may pale in significance compared to the revolution an efficient method for solving NP-complete problems would cause in mathematics itself. According to Stephen Cook,

...it would transform mathematics by allowing a computer to find a formal proof of any theorem which has a proof of a reasonable length, since formal proofs can easily be recognized in polynomial time. Example problems may well include all of the CMI prize problems.

Research mathematicians spend their careers trying to prove theorems, and some proofs have taken decades or even centuries to find after problems have been stated – for instance, Fermat's Last Theorem took over three centuries to prove. A method that is guaranteed to find proofs to theorems, should one exist of a "reasonable" size, would essentially end this struggle.

A proof that showed that P ≠ NP, while lacking the practical computational benefits of a proof that P = NP, would also represent a very significant advance in computational complexity theory and provide guidance for future research. It would allow one to show in a formal way that many common problems cannot be solved efficiently, so that the attention of researchers can be focused on partial solutions or solutions to other problems. Due to widespread belief in P ≠ NP, much of this focusing of research has already taken place.

Results about difficulty of proof

The Clay Mathematics Institute million-dollar prize and a huge amount of dedicated research with no substantial results suggest that the problem is difficult. Some of the most fruitful research related to the P = NP problem has been in showing that existing proof techniques are not powerful enough to answer the question, thus suggesting that novel technical approaches are required.

As additional evidence for the difficulty of the problem, essentially all known proof techniques in computational complexity theory fall into one of the following classifications, each of which is known to be insufficient to prove that P ≠ NP:

• Relativizing proofs: Imagine a world where every algorithm is allowed to make queries to some fixed subroutine called an oracle, and the running time of the oracle is not counted against the running time of the algorithm. Most proofs (especially classical ones) apply uniformly in a world with oracles regardless of what the oracle does. These proofs are called relativizing. In 1975, Baker, Gill, and Solovay showed that P = NP with respect to some oracles, while P ≠ NP for other oracles. Since relativizing proofs can only prove statements that are uniformly true with respect to all possible oracles, this showed that relativizing techniques cannot resolve P = NP.
• Natural proofs: In 1993, Alexander Razborov and Steven Rudich defined a general class of proof techniques for circuit complexity lower bounds, called natural proofs. At the time all previously known circuit lower bounds were natural, and circuit complexity was considered a very promising approach for resolving P = NP. However, Razborov and Rudich showed that in order to prove P ≠ NP using a natural proof, one necessarily must also prove an even stronger statement, which is believed to be false. Thus it is unlikely that natural proofs alone can resolve P = NP.
• Algebrizing proofs: After the Baker-Gill-Solovay result, new non-relativizing proof techniques were successfully used to prove that IP = PSPACE. However, in 2008, Scott Aaronson and Avi Wigderson showed that the main technical tool used in the IP = PSPACE proof, known as arithmetization, was also insufficient to resolve P = NP.

These barriers are another reason why NP-complete problems are useful: if a polynomial-time algorithm can be demonstrated for an NP-complete problem, this would solve the P = NP problem in a way which is not excluded by the above results.

These barriers have also led some computer scientists to suggest that the P versus NP problem may be independent of standard axiom systems like ZFC (cannot be proved or disproved within them). The interpretation of an independence result could be that either no polynomial-time algorithm exists for any NP-complete problem, but such a proof cannot be constructed in (e.g.) ZFC, or that polynomial-time algorithms for NP-complete problems may exist, but it's impossible to prove in ZFC that such algorithms are correct. However, if it can be shown, using techniques of the sort that are currently known to be applicable, that the problem cannot be decided even with much weaker assumptions extending the Peano axioms (PA) for integer arithmetic, then there would necessarily exist nearly-polynomial-time algorithms for every problem in NP. Therefore, if one believes (as most complexity theorists do) that problems in NP do not have efficient algorithms, it would follow that proofs of independence using those techniques cannot be possible. Additionally, this result implies that proving independence from PA or ZFC using currently known techniques is no easier than proving the existence of efficient algorithms for all problems in NP.

Notable attempts at proof

There have been numerous attempts at proving a solution to the problem. The following attempts have received significant coverage:

• On 6 August 2010, Vinay Deolalikar sent a manuscript to various researchers claiming to contain a proof that P ≠ NP. The proof is still being reviewed by other academics. The most notable comment so far was made by Neil Immerman, claiming that there are at least two fatal flaws in the proof.

Logical characterizations

The P = NP problem can be restated in terms of the expressibility of certain classes of logical statements, as a result of work in descriptive complexity. All languages (of finite structures with a fixed signature including a linear order relation) in P can be expressed in first-order logic with the addition of a suitable least fixed point operator (effectively, this, in combination with the order, allows the definition of recursive functions); indeed, (as long as the signature contains at least one predicate or function in addition to the distinguished order relation [so that the amount of space taken to store such finite structures is actually polynomial in the number of elements in the structure]), this precisely characterizes P. Similarly, NP is the set of languages expressible in existential second-order logic — that is, second-order logic restricted to exclude universal quantification over relations, functions, and subsets. The languages in the polynomial hierarchy, PH, correspond to all of second-order logic. Thus, the question "is P a proper subset of NP" can be reformulated as "is existential second-order logic able to describe languages (of finite linearly ordered structures with nontrivial signature) that first-order logic with least fixed point cannot?". The word "existential" can even be dropped from the previous characterization, since P = NP if and only if P = PH (as the former would establish that NP = co-NP, which in turn would imply that NP = PH). PSPACE = NPSPACE as established Savitch's theorem, this follows directly from the fact that the square of a polynomial function is still a polynomial function. However, it is believed, but not proven, a similar relationship may not exist between the polynomial time complexity classes, P and NP so the question is still open.

Polynomial-time algorithms

No algorithm for any NP-complete problem is known to run in polynomial time. However, there are algorithms for NP-complete problems with the property that if P = NP, then the algorithm runs in polynomial time (although with enormous constants, making the algorithm impractical). The following algorithm, due to Levin, is such an example. It correctly accepts the NP-complete language SUBSET-SUM, and runs in polynomial time if and only if P = NP:

// Algorithm that accepts the NP-complete language SUBSET-SUM.
//
// This is a polynomial-time algorithm if and only if P=NP.
//
// "Polynomial-time" means it returns "yes" in polynomial time when
// the answer should be "yes", and runs forever when it is "no".
//
// Input: S = a finite set of integers
// Output: "yes" if any subset of S adds up to 0.
// Runs forever with no output otherwise.
// Note: "Program number P" is the program obtained by
// writing the integer P in binary, then
// considering that string of bits to be a
// program. Every possible program can be
// generated this way, though most do nothing
// because of syntax errors.

FOR N = 1...infinity
FOR P = 1...N
Run program number P for N steps with input S
IF the program outputs a list of distinct integers
AND the integers are all in S
AND the integers sum to 0

THEN
OUTPUT "yes" and HALT

If, and only if, P = NP, then this is a polynomial-time algorithm accepting an NP-complete language. "Accepting" means it gives "yes" answers in polynomial time, but is allowed to run forever when the answer is "no".

Note that this is enormously impractical, even if P = NP. If the shortest program that can solve SUBSET-SUM in polynomial time is b bits long, the above algorithm will try 2^b−1 other programs first.

Perhaps we want to "solve" the SUBSET-SUM problem, rather than just "accept" the SUBSET-SUM language. That means we want the algorithm to always halt and return a "yes" or "no" answer. If P = NP, then there is an algorithm which does this in polynomial time, which uses some polynomial-time verification method that there is no subset sum in the algorithm above.

Formal definitions for P and NP

Conceptually a decision problem is a problem that takes as input some string $w$ over an alphabet $\Sigma$, and outputs "yes" or "no". If there is an algorithm (say a Turing machine, or a computer program with unbounded memory) which is able to produce the correct answer for any input string of length $n$ in at most $c\cdot n^{k}$ steps, where $k$ and $c$ are constants independent of the input string, then we say that the problem can be solved in polynomial time and we place it in the class P. Formally, P is defined as the set of all languages which can be decided by a deterministic polynomial-time Turing machine. That is,

P = $\{L:L=L(M){\text{ for some deterministic polynomial-time Turing machine }}M\}$

where $L(M)=\{w\in \Sigma ^{*}:M{\text{ accepts }}w\}$

and a deterministic polynomial-time Turing machine is a deterministic Turing machine $M$ which satisfies the following two conditions:

1. $M{\text{ halts on all input }}w$; and
2. there exists $k\in N$ such that $T_{M}(n)\in \;$O$(n^{k})$,

where $T_{M}(n)=\max\{t_{M}(w):w\in \Sigma ^{*},\left|w\right|=n\}$

and $t_{M}(w)={\text{ number of steps M takes to halt on input }}w.$

NP can be defined similarly using nondeterministic Turing machines (the traditional way). However, a modern approach to define NP is to use the concept of certificate and verifier. Formally, NP is defined as the set of languages over a finite alphabet that have a verifier that runs in polynomial time, where the notion of "verifier" is defined as follows.

Let $L$ be a language over a finite alphabet, $\Sigma$.

$L\in \mathbf {NP}$ if, and only if, there exists a binary relation $R\subset \Sigma ^{*}\times \Sigma ^{*}$ and a positive integer $k$ such that the following two conditions are satisfied:

1. For all $x\in \Sigma ^{*}$, $x\in L\Leftrightarrow \exists y\in \Sigma ^{*}$ such that $(x,y)\in R\;$ and $\left|y\right|\in \;$O$(\left|x\right|^{k})$; and
2. the language $L_{R}=\{x\#y:(x,y)\in R\}$ over $\Sigma \cup \{\#\}$ is decidable by a Turing machine in polynomial time.

A Turing machine that decides $L_{R}$ is called a verifier for $L$ and a $y$ such that $(x,y)\in R$ is called a certificate of membership of $x$ in $L$.

In general, a verifier does not have to be polynomial-time. However, for $L$ to be in NP, there must be a verifier that runs in polynomial time.

Formal definition for NP-completeness

There are many equivalent ways of describing NP-completeness.

Let $\ L$ be a language over a finite alphabet $\ \Sigma$.

$\ L$ is NP-complete if, and only if, the following two conditions are satisfied:

1. $L\in \mathbf {NP}$; and
2. any $L^{'}\in \mathbf {NP}$ is polynomial-time-reducible to $\ L$ (written as $L^{'}\leq _{p}L$), where $L^{'}\leq _{p}L$ if, and only if, the following two conditions are satisfied:
   1. There exists $f:\Sigma ^{*}\rightarrow \Sigma ^{*}$ such that $\forall w\in \Sigma ^{*}(w\in L^{'}\Leftrightarrow f(w)\in L)$; and
   2. there exists a polynomial-time Turing machine which halts with $\ f(w)$ on its tape on any input $\ w$.

See also

• Game complexity
• Unsolved problems in computer science
• Unsolved problems in mathematics

Further reading

• A. S. Fraenkel and D. Lichtenstein, Computing a perfect strategy for n*n chess requires time exponential in n, Proc. 8th Int. Coll. Automata, Languages, and Programming, Springer LNCS 115 (1981) 278–293 and J. Comb. Th. A 31 (1981) 199–214.
• E. Berlekamp and D. Wolfe, Mathematical Go: Chilling Gets the Last Point, A. K. Peters, 1994. D. Wolfe, Go endgames are hard, MSRI Combinatorial Game Theory Research Worksh., 2000.
• Neil Immerman. Languages Which Capture Complexity Classes. 15th ACM STOC Symposium, pp. 347–354. 1983.
• Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein (2001). "Chapter 34: NP-Completeness". Introduction to Algorithms (Second ed.). MIT Press and McGraw-Hill. pp. 966–1021. ISBN 0-262-03293-7.{{cite book}}: CS1 maint: multiple names: authors list (link)
• Christos Papadimitriou (1993). "Chapter 14: On P vs. NP". Computational Complexity (1st ed.). Addison Wesley. pp. 329–356. ISBN 0-201-53082-1.
• Lance Fortnow (September 2009), "The Status of the P Versus NP Problem", Communications of the ACM, vol. 52, no. 9, pp. 78–86, doi:10.1145/1562164.1562186

External links

• The Clay Mathematics Institute Millennium Prize Problems
• Template:PDF
• Ian Stewart on Minesweeper as NP-complete at The Clay Math Institute
• Gerhard J. Woeginger. The P-versus-NP page. A list of links to a number of purported solutions to the problem. Some of these links state that P equals NP, some of them state the opposite. It is probable that all these alleged solutions are incorrect.
• Computational Complexity of Games and Puzzles
• Complexity Zoo: Class P, Complexity Zoo: Class NP
• Scott Aaronson 's Shtetl Optimized blog: Reasons to believe, a list of justifications for the belief that P ≠ NP