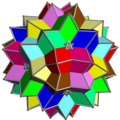
Compound of ten octahedra
Appearance
(Redirected from Octahedron 10-compound)
| Compounds of ten octahedra | |
|---|---|
| |
| Type | Uniform compound |
| Index | UC15 and UC16 |
| Polyhedra | 10 octahedra |
| Faces | 20+60 triangles |
| Edges | 120 |
| Vertices | 60 |
| Symmetry group | icosahedral (Ih) |
| Subgroup restricting to one constituent | 3-fold antiprismatic (D3d) |

The compounds of ten octahedra UC15 and UC16 are two uniform polyhedron compounds. They are composed of a symmetric arrangement of 10 octahedra, considered as triangular antiprisms, aligned with the axes of three-fold rotational symmetry of an icosahedron. The two compounds differ in the orientation of their octahedra: each compound may be transformed into the other by rotating each octahedron by 60 degrees.
Cartesian coordinates
[edit]Cartesian coordinates for the vertices of this compound are all the cyclic permutations of
- (0, ±(τ−1√2 + 2sτ), ±(τ√2 − 2sτ−1))
- (±(√2 − sτ2), ±(√2 + s(2τ − 1)), ±(√2 + sτ−2))
- (±(τ−1√2 − sτ), ±(τ√2 + sτ−1), ±3s)
where τ = (1 + √5)/2 is the golden ratio (sometimes written φ) and s is either +1 or −1. Setting s = −1 gives UC15, while s = +1 gives UC16.
See also
[edit]- Compound of three octahedra
- Compound of four octahedra
- Compound of five octahedra
- Compound of twenty octahedra
References
[edit]- Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79 (3): 447–457, doi:10.1017/S0305004100052440, MR 0397554.

