Jump to content

Letter frequency: Difference between revisions

From Wikipedia, the free encyclopedia
Browse history interactively
← Previous editNext edit →
Content deleted Content added
VisualWikitext
No edit summary
No edit summary
Line 1: Line 1:
The '''frequency of letters''' in text has often been studied for use in [[cryptanalysis]], and [[frequency analysis]] in particular. No exact letter frequency distribution underlies a given language, since all writers write slightly differently. [[Linotype machine]]s assumed the letter order, from most to least common, to be '''[[ETAOIN SHIDLU|etaoin shitlu]] cmfwyp vbgkjq xz''' based on the experience and custom of manual compositors. Likewise, [[Morse code|Modern International Morse code]] encodes the most frequent letters with the shortest symbols; arranging the Morse alphabet into groups of letters that require equal amounts of time to transmit, and then sorting these groups in increasing order, yields '''e it san hurdm wgvlfbk opjxcz yq'''. Similar ideas are used in modern data-compression techniques such as [[Huffman coding]].
The '''frequency of letters''' in text has often been studied for use in [[cryptanalysis]], and [[frequency analysis]] in particular. No exact letter frequency distribution underlies a given language, since all writers write slightly differently. [[Linotype machine]]s assumed the letter order, from most to least common, to be '''[[ETAOIN SHIDLU|etaoin shidlu]] cmfwyp vbgkjq xz''' based on the experience and custom of manual compositors. Likewise, [[Morse code|Modern International Morse code]] encodes the most frequent letters with the shortest symbols; arranging the Morse alphabet into groups of letters that require equal amounts of time to transmit, and then sorting these groups in increasing order, yields '''e it san hurdm wgvlfbk opjxcz yq'''. Similar ideas are used in modern data-compression techniques such as [[Huffman coding]].


==Introduction==
==Introduction==

Revision as of 18:27, 7 April 2014

The frequency of letters in text has often been studied for use in cryptanalysis, and frequency analysis in particular. No exact letter frequency distribution underlies a given language, since all writers write slightly differently. Linotype machines assumed the letter order, from most to least common, to be etaoin shidlu cmfwyp vbgkjq xz based on the experience and custom of manual compositors. Likewise, Modern International Morse code encodes the most frequent letters with the shortest symbols; arranging the Morse alphabet into groups of letters that require equal amounts of time to transmit, and then sorting these groups in increasing order, yields e it san hurdm wgvlfbk opjxcz yq. Similar ideas are used in modern data-compression techniques such as Huffman coding.

Introduction

Letter frequencies, like word frequencies, tend to vary, both by writer and by subject. One cannot write an essay about x-rays without using frequent Xs, and the essay will have an idiosyncratic letter frequency if the essay is about the frequent use of x-rays to treat zebras in Qatar. Different authors have habits which can be reflected in their use of letters. Hemingway's writing style, for example, is visibly different from Faulkner's. Letter, bigram, trigram, word frequencies, word length, and sentence length can be calculated for specific authors, and used to prove or disprove authorship of texts, even for authors whose styles are not so divergent.

Accurate average letter frequencies can only be gleaned by analyzing a large amount of representative text. With the availability of modern computing and collections of large text corpora, such calculations are easily made. Examples can be drawn from a variety of sources (press reporting, religious texts, scientific texts and general fiction) and there are differences especially for general fiction with the position of 'h' and 'i', with H becoming more common.

Herbert S. Zim, in his classic introductory cryptography text "Codes and Secret Writing", gives the English letter frequency sequence as "ETAON RISHD LFCMU GYPWB VKJXQ Z", the most common letter pairs as "TH HE AN RE ER IN ON AT ND ST ES EN OF TE ED OR TI HI AS TO", and the most common doubled letters as "LL EE SS OO TT FF RR NN PP CC".[1]

The "top twelve" letters comprise about 80% of the total usage. The "top eight" letters comprise about 65% of the total usage. Letter frequency as a function of rank can be fitted well by several rank functions, with the two-parameter Cocho/Beta rank function being the best.[2] Another rank function with no adjustable free parameter also fits the letter frequency distribution reasonably well[3] (the same function has been used to fit the amino acid frequency in protein sequences.[4]) A spy using the VIC cipher or some other cipher based on a straddling checkerboard typically uses a mnemonic such as "a sin to err" (dropping the second "r") to remember the top eight characters.

The use of letter frequencies and frequency analysis plays a fundamental role in cryptograms and several word puzzle games, including Hangman, Scrabble and the television game show Wheel of Fortune. One of the earliest description in classical literature of applying the knowledge of English letter frequency to solving a cryptogram is found in E.A. Poe's famous story The Gold-Bug, where the method is successfully applied to decipher a message instructing on the whereabouts of a treasure hidden by Captain Kidd.[5]

Letter frequencies had a strong effect on the design of some keyboard layouts. The most-frequent letters are on the bottom row of the Blickensderfer typewriter, and the home row of the Dvorak Simplified Keyboard.

Relative frequencies of letters in the English language

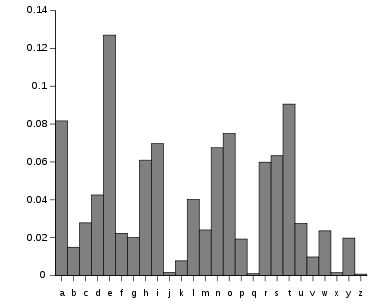
Relative frequencies of letters in text.
Relative frequencies ordered by frequency.

Analysis of entries in the Concise Oxford dictionary is published by the compilers.[6] The table below is taken from Pavel Mička's website, which cites Robert Lewand's Cryptological Mathematics.[7]

Letter Relative frequency in the English language
a 8.167% 8.167
 
b 1.492% 1.492
 
c 2.782% 2.782
 
d 4.253% 4.253
 
e 12.702% 12.702
 
f 2.228% 2.228
 
g 2.015% 2.015
 
h 6.094% 6.094
 
i 6.966% 6.966
 
j 0.153% 0.153
 
k 0.772% 0.772
 
l 4.025% 4.025
 
m 2.406% 2.406
 
n 6.749% 6.749
 
o 7.507% 7.507
 
p 1.929% 1.929
 
q 0.095% 0.095
 
r 5.987% 5.987
 
s 6.327% 6.327
 
t 9.056% 9.056
 
u 2.758% 2.758
 
v 0.978% 0.978
 
w 2.360% 2.36
 
x 0.150% 0.15
 
y 1.974% 1.974
 
z 0.074% 0.074
 

This table differs slightly from others,[how?] such as Cornell University Math Explorer's Project, which produced a table after measuring 40,000 words.[8]

In English, the space is slightly more frequent than the top letter (e) [9] and the non-alphabetic characters (digits, punctuation, etc.) collectively occupy the fourth position, between t and a.[10]

Relative frequencies of the first letters of a word in the English language

Analysis of a subset of Project Gutenberg text shows the following frequencies of letters at the starts of words:[11]

Letter Relative frequency as the first letter of an English word
a 11.602% 11.602
 
b 4.702% 4.702
 
c 3.511% 3.511
 
d 2.670% 2.67
 
e 2.007% 2.007
 
f 3.779% 3.779
 
g 1.950% 1.95
 
h 7.232% 7.232
 
i 6.286% 6.286
 
j 0.597% 0.597
 
k 0.590% 0.59
 
l 2.705% 2.705
 
m 4.374% 4.374
 
n 2.365% 2.365
 
o 6.264% 6.264
 
p 2.545% 2.545
 
q 0.173% 0.173
 
r 1.653% 1.653
 
s 7.755% 7.755
 
t 16.671% 16.671
 
u 1.487% 1.487
 
v 0.649% 0.649
 
w 6.753% 6.753
 
x 0.037% 0.037
 
y 1.620% 1.62
 
z 0.034% 0.034
 

Relative frequencies of letters in other languages

Letter French [12] German [13] Spanish [14] Portuguese [15] Esperanto [16] Italian[17] Turkish Swedish[18] Polish[19] Dutch [20] Danish[21] Icelandic[22] Finnish[23]
a 7.636% 6.516% 12.525% 14.634% 12.117% 11.745% 11.680% 9.383% 11.503% 7.486% 6.025% 10.110% 12.217%
b 0.901% 1.886% 2.215% 1.043% 0.980% 0.927% 2.952% 1.535% 1.740% 1.584% 2.000% 1.043% 0.281%
c 3.260% 2.732% 4.139% 3.882% 0.776% 4.501% 0.970% 1.486% 3.895% 1.242% 0.565% 0 0.281%
d 3.669% 5.076% 5.860% 4.992% 3.044% 3.736% 4.871% 4.702% 4.225% 5.933% 5.858% 1.575% 1.043%
e 14.715% 17.396% 13.681% 12.570% 8.995% 11.792% 9.007% 10.149% 8.352% 18.914% 15.453% 6.418% 7.968%
f 1.066% 1.656% 0.692% 1.023% 1.037% 1.153% 0.444% 2.027% 0.143% 0.805% 2.406% 3.013% 0.194%
g 0.866% 3.009% 1.768% 1.303% 1.171% 1.644% 1.340% 2.862% 1.731% 3.403% 4.077% 4.241% 0.392%
h 0.737% 4.757% 0.703% 0.781% 0.384% 0.636% 1.145% 2.090% 1.015% 2.380% 1.621% 1.871% 1.851%
i 7.529% 7.550% 6.247% 6.186% 10.012% 11.283% 8.274%* 5.817% 9.328% 6.499% 6.000% 7.578% 10.817%
j 0.545% 0.268% 0.443% 0.397% 3.501% 0.011% 0.046% 0.614% 1.836% 1.461% 0.730% 1.144% 2.042%
k 0.049% 1.417% 0.011% 0.015% 4.163% 0.009% 4.715% 3.140% 2.753% 2.248% 3.395% 3.314% 4.973%
l 5.456% 3.437% 4.967% 2.779% 6.145% 6.510% 5.752% 5.275% 3.064% 3.568% 5.229% 4.532% 5.761%
m 2.968% 2.534% 3.157% 4.738% 2.994% 2.512% 3.745% 3.471% 2.515% 2.213% 3.237% 4.041% 3.202%
n 7.095% 9.776% 6.712% 5.046% 7.955% 6.883% 7.231% 8.542% 6.737% 10.032% 7.240% 7.711% 8.826%
o 5.378% 2.594% 8.683% 10.735% 8.779% 9.832% 2.653% 4.482% 7.167% 6.063% 4.636% 2.166% 5.614%
p 2.521% 0.670% 2.510% 2.523% 2.745% 3.056% 0.788% 1.839% 2.445% 1.370% 1.756% 0.789% 1.842%
q 1.362% 0.018% 0.877% 1.204% 0 0.505% 0 0.020% 0 0.009% 0.007% 0 0.013%
r 6.553% 7.003% 6.871% 6.530% 5.914% 6.367% 6.948% 8.431% 5.743% 6.411% 8.956% 8.581% 2.872%
s 7.948% 7.273% 7.977% 7.805% 6.092% 4.981% 2.950% 6.590% 6.224% 5.733% 5.805% 5.630% 7.862%
t 7.244% 6.154% 4.632% 4.736% 5.276% 5.623% 3.049% 7.691% 2.475% 6.923% 6.862% 4.953% 8.750%
u 6.311% 4.346% 3.927% 4.634% 3.183% 3.011% 3.430% 1.919% 2.062% 2.192% 1.979% 4.562% 5.008%
v 1.628% 0.846% 1.138% 1.665% 1.904% 2.097% 0.977% 2.415% 0 1.854% 2.332% 2.437% 2.250%
w 0.074% 1.921% 0.017% 0.037% 0 0.033% 0.016% 0.142% 6.313% 1.821% 0.069% 0 0.094%
x 0.427% 0.034% 0.215% 0.253% 0 0 0.007% 0.159% 0 0.036% 0.028% 0.046% 0.031%
y 0.128% 0.039% 1.008% 0.006% 0 0.020% 3.371% 0.708% 3.206% 0.035% 0.698% 0.900% 1.745%
z 0.326% 1.134% 0.517% 0.470% 0.494% 1.181% 1.497% 0.070% 5.852% 1.374% 0.034% 0 0.051%
à 0.486% 0 0 0.072% 0 0.635% 0 0 0 0 0 0 0
â 0.051% 0 0 0.562% 0 0 0 0 0 0 0 0 0
á 0 0 0.502% 0.118% 0 0 0 0 0 0 0 1.799% 0
å 0 0 0 0 0 0 0 1.338% 0 0 1.190% 0 0.003%
ä 0 0.447% 0 0 0 0 0 1.797% 0 0 0 0 3.577%
ã 0 0 0 0.733% 0 0 0 0 0 0 0 0 0
ą 0 0 0 0 0 0 0 0 0.699% 0 0 0 0
æ 0 0 0 0 0 0 0 0 0 0 0.872% 0.867% 0
œ 0.018% 0 0 0 0 0 0 0 0 0 0 0 0
ç 0.085% 0 0 0.530% 0 0 0.825% 0 0 0 0 0 0
ĉ 0 0 0 0 0.657% 0 0 0 0 0 0 0 0
ć 0 0 0 0 0 0 0 0 0.743% 0 0 0 0
ð 0 0 0 0 0 0 0 0 0 0 0 4.393% 0
è 0.271% 0 0 0 0 0.263% 0 0 0 0 0 0 0
é 1.504% 0 0.433% 0.337% 0 0 0 0 0 0 0 0.647% 0
ê 0.225% 0 0 0.450% 0 0 0 0 0 0 0 0 0
ë 0.001% 0 0 0 0 0 0 0 0 0 0 0 0
ę 0 0 0 0 0 0 0 0 1.035% 0 0 0 0
ĝ 0 0 0 0 0.691% 0 0 0 0 0 0 0 0
ğ 0 0 0 0 0 0 1.129% 0 0 0 0 0 0
ĥ 0 0 0 0 0.022% 0 0 0 0 0 0 0 0
î 0.045% 0 0 0 0 0 0 0 0 0 0 0 0
ì 0 0 0 0 0 0.030% 0 0 0 0 0 0 0
í 0 0 0.725% 0.132% 0 0 0 0 0 0 0 1.570% 0
ï 0.005% 0 0 0 0 0 0 0 0 0 0 0 0
ı 0 0 0 0 0 0 5.199%* 0 0 0 0 0 0
ĵ 0 0 0 0 0.055% 0 0 0 0 0 0 0 0
ł 0 0 0 0 0 0 0 0 2.109% 0 0 0 0
ñ 0 0 0.311% 0 0 0 0 0 0 0 0 0 0
ń 0 0 0 0 0 0 0 0 0.362% 0 0 0 0
ò 0 0 0 0 0 0.002% 0 0 0 0 0 0 0
ö 0 0.573% 0 0 0 0 0.270% 1.305% 0 0 0 0.777% 0.444%
ô 0.023% 0 0 0.635% 0 0 0 0 0 0 0 0 0
ó 0 0 0.827% 0.296% 0 0 0 0 1.141% 0 0 0.994% 0
ø 0 0 0 0 0 0 0 0 0 0 0.939% 0 0
ŝ 0 0 0 0 0.385% 0 0 0 0 0 0 0 0
ş 0 0 0 0 0 0 1.938% 0 0 0 0 0 0
ś 0 0 0 0 0 0 0 0 0.814% 0 0 0 0
ß 0 0.307% 0 0 0 0 0 0 0 0 0 0 0
þ 0 0 0 0 0 0 0 0 0 0 0 1.455% 0
ù 0.058% 0 0 0 0 0.166% 0 0 0 0 0 0 0
ú 0 0 0.168% 0.207% 0 0 0 0 0 0 0 0.613% 0
ŭ 0 0 0 0 0.520% 0 0 0 0 0 0 0 0
ü 0 0.995% 0.012% 0.026% 0 0 1.992% 0 0 0 0 0 0
ý 0 0 0 0 0 0 0 0 0 0 0 0.228% 0
ź 0 0 0 0 0 0 0 0 0.078% 0 0 0 0
ż 0 0 0 0 0 0 0 0 0.706% 0 0 0 0

*See Dotted and dotless I

The figure below illustrates the frequency distributions of the 26 most common Latin letters across some languages. Template:Letter frequencies in 14 languages

Based on these tables, the 'etaoin shrdlu'-equivalent results for each language is as follows:

  • French: 'esait nrulo'; (Indo-European: Romance; traditionally, 'esartinulop' is used, in part for its ease of pronunciation[24])
  • Spanish: 'eaosr nidlt'; (Indo-European: Romance)
  • Portuguese: 'aeosr indmt' (Indo-European: Romance)
  • Italian: 'eaion lrtsc'; (Indo-European: Romance)
  • Esperanto: 'aieon lsrtk' (artificial language – influenced by Indo-European languages, Romance, Germanic mostly)
  • German: 'enisr atdhu'; (Indo-European: Germanic)
  • Swedish: 'eantr sildo'; (Indo-European: Germanic)
  • Turkish: 'aeinr ldkmu'; (Altaic: Turkic)
  • Dutch: 'enati rodsl'; (Indo-European: Germanic)[20]
  • Polish: 'aoien wszrd'; (Indo-European: Slavic)
  • Danish: 'ernta idslo'; (Indo-European: Germanic)
  • Icelandic: 'arnie stulg'; (Indo-European: Germanic)
  • Finnish: 'ainte slouk'; (Indo-European: Finnic)

All these languages use a basically similar 25+ character alphabet.

See also

References

  1. ^ Zim, Herbert Spencer. (1961). Codes & Secret Writing: Authorized Abridgement. Scholastic Book Services. OCLC 317853773.
  2. ^ Li, Wentian; Miramontes, Pedro (2011). "Fitting ranked English and Spanish letter frequency distribution in US and Mexican presidential speeches". Journal of Quantitative Linguistics. 18 (4): 359. doi:10.1080/09296174.2011.608606.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  3. ^ Gusein-Zade, S.M. (1988). "Frequency distribution of letters in the Russian language". Probl. Peredachi Inf. 24 (4): 102–7.
  4. ^ Gamow, George; Ycas, Martynas (1955). "Statistical correlation of protein and ribonucleic acid composition" (PDF). Proc. Natl. Acad. Sci. 41 (12): 1011–19. doi:10.1073/pnas.41.12.1011. PMC 528190.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  5. ^ Poe, Edgar Allan. "The works of Edgar Allan Poe in five volumes". Project Gutenberg.
  6. ^ "What is the frequency of the letters of the alphabet in English?". Oxford Dictionary. Oxford University Press. Retrieved 29 December 2012.
  7. ^ Mička, Pavel. "Letter frequency (English)". Algoritmy.net.
  8. ^ http://www.math.cornell.edu/~mec/2003-2004/cryptography/subs/frequencies.html
  9. ^ Statistical Distributions of English Text
  10. ^ Lee, E. Stewart. "Essays about Computer Security" (PDF). University of Cambridge Computer Laboratory. p. 181.
  11. ^ Calculated from "Project Gutenberg Selections" available from the NLTK Corpora
  12. ^ "CorpusDeThomasTempé". Retrieved 2007-06-15.
  13. ^ Beutelspacher, Albrecht (2005). Kryptologie (7 ed.). Wiesbaden: Vieweg. p. 10. ISBN 3-8348-0014-7.
  14. ^ Pratt, Fletcher (1942). Secret and Urgent: the Story of Codes and Ciphers. Garden City, N.Y.: Blue Ribbon Books. pp. 254–5. OCLC 795065.
  15. ^ "Frequência da ocorrência de letras no Português". Retrieved 2009-06-16.
  16. ^ "La Oftecoj de la Esperantaj Literoj". Retrieved 2007-09-14.
  17. ^ Singh, Simon; Galli, Stefano (1999). Codici e Segreti (in Italian). Milano: Rizzoli. ISBN 978-8-817-86213-4. OCLC 535461359.
  18. ^ "Practical Cryptography". Retrieved 2013-10-30.
  19. ^ Wstęp do kryptologii, counting [space] 17.2%, [dot point] 0.9%, [comma] 0.9% and [semicolon] 0.5%
  20. ^ a b "Letterfrequenties". Genootschap OnzeTaal. Retrieved 2009-05-17.
  21. ^ "Practical Cryptography". Retrieved 2013-10-24.
  22. ^ "Practical Cryptography". Retrieved 2013-10-24.
  23. ^ "Practical Cryptography". Retrieved 2013-10-24.
  24. ^ Perec, Georges; Alphabets; Éditions Galilée, 1976
Notes

Some useful tables for single letter, digram, trigram, tetragram, and pentagram frequencies based on 20,000 words that take into account word-length and letter-position combinations for words 3 to 7 letters in length. The references are as follows:

  1. Mayzner, M.S.; Tresselt, M.E. (1965). "Tables of single-letter and digram frequency counts for various word-length and letter-position combinations". Psychonomic Monograph Supplements. 1 (2): 13–32. OCLC 639975358.
  2. Mayzner, M.S.; Tresselt, M.E.;Wolin, B.< R.< (1965). "Tables of trigram frequency counts for various word-length and letter-position combinations". Psychonomic Monograph Supplements. 1 (3): 33–78.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  3. Mayzner, M.S.; Tresselt, M.E.;Woliin, B.< R,.. (1965). "Tables of tetragram frequency counts for various word-length and letter-position combinations". Psychonomic Monograph Supplements. 1 (4): 79–143.{{cite journal}}: CS1 maint: multiple names: authors list (link)
  4. Mayzner, M.S.; Tresselt, M.E.Wolin, B,.< R.> (1965). "Tables of pentagram frequency counts for various word-length and letter-position combinations". Psychonomic Monograph Supplements. 1 (5): 144–190.{{cite journal}}: CS1 maint: multiple names: authors list (link)

Template:Link FA

Retrieved from "https://wiki.riteme.site/w/index.php?title=Letter_frequency&oldid=603186997"