Galois/Counter Mode
In cryptography, Galois/Counter Mode (GCM)[1] is a mode of operation for symmetric-key cryptographic block ciphers which is widely adopted for its performance. GCM throughput rates for state-of-the-art, high-speed communication channels can be achieved with inexpensive hardware resources.[2]
The GCM algorithm provides both data authenticity (integrity) and confidentiality and belongs to the class of authenticated encryption with associated data (AEAD) methods. This means that as input it takes a key K, some plaintext P, and some associated data AD; it then encrypts the plaintext using the key to produce ciphertext C, and computes an authentication tag T from the ciphertext and the associated data (which remains unencrypted). A recipient with knowledge of K, upon reception of AD, C and T, can decrypt the ciphertext to recover the plaintext P and can check the tag T to ensure that neither ciphertext nor associated data were tampered with.
GCM uses a block cipher with block size 128 bits (commonly AES-128) operated in counter mode for encryption, and uses arithmetic in the Galois field GF(2128) to compute the authentication tag; hence the name.
Galois Message Authentication Code (GMAC) is an authentication-only variant of the GCM which can form an incremental message authentication code. Both GCM and GMAC can accept initialization vectors of arbitrary length.
Different block cipher modes of operation can have significantly different performance and efficiency characteristics, even when used with the same block cipher. GCM can take full advantage of parallel processing and implementing GCM can make efficient use of an instruction pipeline or a hardware pipeline. By contrast, the cipher block chaining (CBC) mode of operation incurs pipeline stalls that hamper its efficiency and performance.
Basic operation
[edit]Like in normal counter mode, blocks are numbered sequentially, and then this block number is combined with an initialization vector (IV) and encrypted with a block cipher E, usually AES. The result of this encryption is then XORed with the plaintext to produce the ciphertext. Like all counter modes, this is essentially a stream cipher, and so it is essential that a different IV is used for each stream that is encrypted.
The ciphertext blocks are considered coefficients of a polynomial which is then evaluated at a key-dependent point H, using finite field arithmetic. The result is then encrypted, producing an authentication tag that can be used to verify the integrity of the data. The encrypted text then contains the IV, ciphertext, and authentication tag.
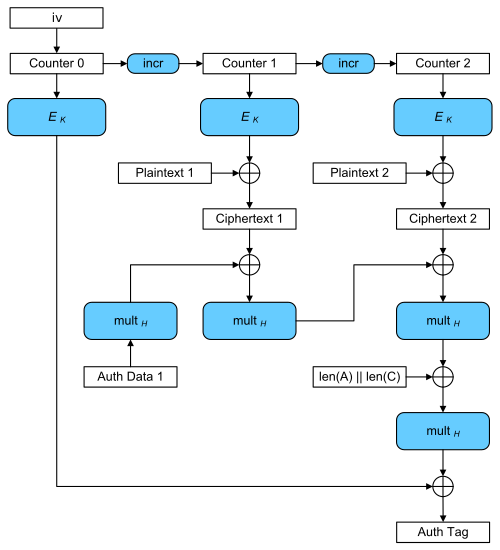
Encryption: A series of 128-bit counters is encrypted using the block cipher E with key K; this can occur in parallel. The results are combined using bitwise XOR with 128-bit plaintext blocks, producing a series of ciphertext blocks.
Authentication: The Additional Data and these ciphertext blocks are combined using multiplication with a key-dependent constant H in the Galois field GF(2128) to produce the authentication tag.
Mathematical basis
[edit]GCM combines the well-known counter mode of encryption with the new Galois mode of authentication. The key feature is the ease of parallel computation of the Galois field multiplication used for authentication. This feature permits higher throughput than encryption algorithms, like CBC, which use chaining modes. The GF(2128) field used is defined by the polynomial
The authentication tag is constructed by feeding blocks of data into the GHASH function and encrypting the result. This GHASH function is defined by
where H = Ek(0128) is the hash key, a string of 128 zero bits encrypted using the block cipher, A is data which is only authenticated (not encrypted), C is the ciphertext, m is the number of 128-bit blocks in A (rounded up), n is the number of 128-bit blocks in C (rounded up), and the variable Xi for i = 0, ..., m + n + 1 is defined below.[3]
First, the authenticated text and the cipher text are separately zero-padded to multiples of 128 bits and combined into a single message Si:
where len(A) and len(C) are the 64-bit representations of the bit lengths of A and C, respectively, v = len(A) mod 128 is the bit length of the final block of A, u = len(C) mod 128 is the bit length of the final block of C, and denotes concatenation of bit strings.
Then Xi is defined as:
The second form is an efficient iterative algorithm (each Xi depends on Xi−1) produced by applying Horner's method to the first. Only the final Xm+n+1 remains an output.
If it is necessary to parallelize the hash computation, this can be done by interleaving k times:
If the length of the IV is not 96, the GHASH function is used to calculate Counter 0:
GCM was designed by John Viega and David A. McGrew to be an improvement to Carter–Wegman counter mode (CWC mode).[4]
In November 2007, NIST announced the release of NIST Special Publication 800-38D Recommendation for Block Cipher Modes of Operation: Galois/Counter Mode (GCM) and GMAC making GCM and GMAC official standards.[5]
Use
[edit]GCM mode is used in the IEEE 802.1AE (MACsec) Ethernet security, WPA3-Enterprise Wifi security protocol, IEEE 802.11ad (also dubbed WiGig), ANSI (INCITS) Fibre Channel Security Protocols (FC-SP), IEEE P1619.1 tape storage, IETF IPsec standards,[6][7] SSH,[8] TLS 1.2[9][10] and TLS 1.3.[11] AES-GCM is included in the NSA Suite B Cryptography and its latest replacement in 2018 Commercial National Security Algorithm (CNSA) suite.[12] GCM mode is used in the SoftEther VPN server and client,[13] as well as OpenVPN since version 2.4.
Performance
[edit]GCM requires one block cipher operation and one 128-bit multiplication in the Galois field per each block (128 bit) of encrypted and authenticated data. The block cipher operations are easily pipelined or parallelized; the multiplication operations are easily pipelined and can be parallelized with some modest effort (either by parallelizing the actual operation, by adapting Horner's method per the original NIST submission, or both).
Intel has added the PCLMULQDQ instruction, highlighting its use for GCM.[14] In 2011, SPARC added the XMULX and XMULXHI instructions, which also perform 64 × 64 bit carry-less multiplication. In 2015, SPARC added the XMPMUL instruction, which performs XOR multiplication of much larger values, up to 2048 × 2048 bit input values producing a 4096-bit result. These instructions enable fast multiplication over GF(2n), and can be used with any field representation.
Impressive performance results are published for GCM on a number of platforms. Käsper and Schwabe described a "Faster and Timing-Attack Resistant AES-GCM"[15] that achieves 10.68 cycles per byte AES-GCM authenticated encryption on 64-bit Intel processors. Dai et al. report 3.5 cycles per byte for the same algorithm when using Intel's AES-NI and PCLMULQDQ instructions. Shay Gueron and Vlad Krasnov achieved 2.47 cycles per byte on the 3rd generation Intel processors. Appropriate patches were prepared for the OpenSSL and NSS libraries.[16]
When both authentication and encryption need to be performed on a message, a software implementation can achieve speed gains by overlapping the execution of those operations. Performance is increased by exploiting instruction-level parallelism by interleaving operations. This process is called function stitching,[17] and while in principle it can be applied to any combination of cryptographic algorithms, GCM is especially suitable. Manley and Gregg[18] show the ease of optimizing when using function stitching with GCM. They present a program generator that takes an annotated C version of a cryptographic algorithm and generates code that runs well on the target processor.
GCM has been criticized in the embedded world (for example by Silicon Labs) because the parallel processing is not suited for performant use of cryptographic hardware engines. As a result, GCM reduces the performance of encryption for some of the most performance-sensitive devices.[19] Specialized hardware accelerators for ChaCha20-Poly1305 are less complex compared to AES accelerators.[20]
Patents
[edit]According to the authors' statement, GCM is unencumbered by patents.[21]
Security
[edit]GCM is proven secure in the concrete security model.[22] It is secure when it is used with a block cipher that is indistinguishable from a random permutation; however, security depends on choosing a unique initialization vector for every encryption performed with the same key (see stream cipher attack). For any given key and initialization vector value, GCM is limited to encrypting 239 − 256 bits of plain text (64 GiB). NIST Special Publication 800-38D[5] includes guidelines for initialization vector selection and limits the number of possible initialization vector values for a single key. As the security assurance of GCM degrades with more data being processed using the same key, the total number of blocks of plaintext and AD protected during the lifetime of a single key should be limited by 264.[5]
The authentication strength depends on the length of the authentication tag, like with all symmetric message authentication codes. The use of shorter authentication tags with GCM is discouraged. The bit-length of the tag, denoted t, is a security parameter. In general, t may be any one of the following five values: 128, 120, 112, 104, or 96. For certain applications, t may be 64 or 32, but the use of these two tag lengths constrains the length of the input data and the lifetime of the key. Appendix C in NIST SP 800-38D provides guidance for these constraints (for example, if t = 32 and the maximal packet size is 210 bytes, the authentication decryption function should be invoked no more than 211 times; if t = 64 and the maximal packet size is 215 bytes, the authentication decryption function should be invoked no more than 232 times).
Like with any message authentication code, if the adversary chooses a t-bit tag at random, it is expected to be correct for given data with probability measure 2−t. With GCM, however, an adversary can increase their likelihood of success by choosing tags with n words – the total length of the ciphertext plus any additional authenticated data (AAD) – with probability measure 2−t by a factor of n. Although, one must bear in mind that these optimal tags are still dominated by the algorithm's survival measure 1 − n⋅2−t for arbitrarily large t. Moreover, GCM is neither well-suited for use with very short tag-lengths nor very long messages.
Ferguson and Saarinen independently described how an attacker can perform optimal attacks against GCM authentication, which meet the lower bound on its security. Ferguson showed that, if n denotes the total number of blocks in the encoding (the input to the GHASH function), then there is a method of constructing a targeted ciphertext forgery that is expected to succeed with a probability of approximately n⋅2−t. If the tag length t is shorter than 128, then each successful forgery in this attack increases the probability that subsequent targeted forgeries will succeed, and leaks information about the hash subkey, H. Eventually, H may be compromised entirely and the authentication assurance is completely lost.[23]
Independent of this attack, an adversary may attempt to systematically guess many different tags for a given input to authenticated decryption and thereby increase the probability that one (or more) of them, eventually, will be considered valid. For this reason, the system or protocol that implements GCM should monitor and, if necessary, limit the number of unsuccessful verification attempts for each key.
Saarinen described GCM weak keys.[24] This work gives some valuable insights into how polynomial hash-based authentication works. More precisely, this work describes a particular way of forging a GCM message, given a valid GCM message, that works with probability of about n⋅2−128 for messages that are n × 128 bits long. However, this work does not show a more effective attack than was previously known; the success probability in observation 1 of this paper matches that of lemma 2 from the INDOCRYPT 2004 analysis (setting w = 128 and l = n × 128). Saarinen also described a GCM variant Sophie Germain Counter Mode (SGCM) based on Sophie Germain primes.
See also
[edit]References
[edit]- ^ RFC 256 AES Galois Counter Mode (GCM) Cipher Suites for TLS
- ^ Lemsitzer, S.; Wolkerstorfer, J.; Felber, N.; Braendli, M. (2007). Paillier, P.; Verbauwhede, I. (eds.). Cryptographic Hardware and Embedded Systems - CHES 2007 . GCM-AES Architecture Optimized for FPGAs. Lecture Notes in Computer Science. Vol. 4727. Springer. pp. 227–238. doi:10.1007/978-3-540-74735-2_16. ISBN 978-3-540-74734-5.
- ^ McGrew, David A.; Viega, John (2005). "The Galois/Counter Mode of Operation (GCM)" (PDF). p. 5. Retrieved 20 July 2013. Note that there is a typo in the formulas in the article.
- ^ Kohno, Tadayoshi; Viega, John; Whiting, Doug (2004). "CWC: A High-Performance Conventional Authenticated Encryption Mode". In Roy, Bimal; Meier, Willi (eds.). Fast Software Encryption. Lecture Notes in Computer Science. Vol. 3017. Berlin, Heidelberg: Springer. pp. 408–426. doi:10.1007/978-3-540-25937-4_26. ISBN 978-3-540-25937-4.
- ^ a b c Dworkin, Morris (2007–2011). Recommendation for Block Cipher Modes of Operation: Galois/Counter Mode (GCM) and GMAC (PDF) (Technical report). NIST. 800-38D. Retrieved 2015-08-18.
- ^ RFC 4106 The Use of Galois/Counter Mode (GCM) in IPsec Encapsulating Security Payload (ESP)
- ^ RFC 4543 The Use of Galois Message Authentication Code (GMAC) in IPsec ESP and AH
- ^ RFC 5647 AES Galois Counter Mode for the Secure Shell Transport Layer Protocol
- ^ RFC 5288 AES Galois Counter Mode (GCM) Cipher Suites for TLS
- ^ RFC 6367 Addition of the Camellia Cipher Suites to Transport Layer Security (TLS)
- ^ RFC 8446 The Transport Layer Security protocol version 1.3
- ^ "Algorithm Registration - Computer Security Objects Register | CSRC | CSRC". 24 May 2016.
- ^ "Why SoftEther VPN – SoftEther VPN Project".
- ^ Gueron, Shay; Kounavis, Michael (April 2014). "Intel Carry-Less Multiplication Instruction and its Usage for Computing the GCM Mode (Revision 2.02)" (PDF). Retrieved 2023-09-01.
- ^ Käsper, E.; Schwabe, P. (2009). "Faster and Timing-Attack Resistant AES-GCM". In Clavier, C.; Gaj, K. (eds.). Cryptographic Hardware and Embedded Systems - CHES 2009. Lecture Notes in Computer Science. Vol. 5747. Springer. pp. 1–17. doi:10.1007/978-3-642-04138-9_1. ISBN 978-3-642-04138-9.
- ^ Gueron, Shay. "AES-GCM for Efficient Authenticated Encryption – Ending the Reign of HMAC-SHA-1?" (PDF). Workshop on Real-World Cryptography. Retrieved 8 February 2013.
- ^ Gopal, V., Feghali, W., Guilford, J., Ozturk, E., Wolrich, G., Dixon, M., Locktyukhin, M., Perminov, M. "Fast Cryptographic Computation on Intel Architecture via Function Stitching" Intel Corp. (2010)
- ^ Manley, Raymond; Gregg, David (2010). "A Program Generator for Intel AES-NI Instructions". In Gong, G.; Gupta, K.C. (eds.). Progress in Cryptology - INDOCRYPT 2010. Lecture Notes in Computer Science. Vol. 6498. Springer. pp. 311–327. doi:10.1007/978-3-642-17401-8_22. ISBN 978-3-642-17400-1.
- ^ "IoT Security Part 6: Galois Counter Mode". 2016-05-06. Retrieved 2023-10-17.
- ^ Pfau, Johannes; Reuter, Maximilian; Harbaum, Tanja; Hofmann, Klaus; Becker, Jurgen (September 2019). "A Hardware Perspective on the ChaCha Ciphers: Scalable Chacha8/12/20 Implementations Ranging from 476 Slices to Bitrates of 175 Gbit/s": 294–299. doi:10.1109/SOCC46988.2019.1570548289.
{{cite journal}}: Cite journal requires|journal=(help) - ^ McGrew, David A.; Viega, John. "The Galois/Counter Mode of Operation (GCM) Intellectual Property Statement" (PDF). Computer Security Resource Center, NIST.
- ^ McGrew, David A.; Viega, John (2004). "The Security and Performance of the Galois/counter mode (GCM) of Operation". Proceedings of INDOCRYPT 2004. Lecture Notes in Computer Science. Vol. 3348. Springer. CiteSeerX 10.1.1.1.4591. doi:10.1007/978-3-540-30556-9_27. ISBN 978-3-540-30556-9.
- ^ Niels Ferguson, Authentication Weaknesses in GCM, 2005-05-20
- ^ Markku-Juhani O. Saarinen (2011-04-20). "Cycling Attacks on GCM, GHASH and Other Polynomial MACs and Hashes". Cryptology ePrint Archive. FSE 2012.
External links
[edit]- NIST Special Publication SP800-38D defining GCM and GMAC
- RFC 4106: The Use of Galois/Counter Mode (GCM) in IPsec Encapsulating Security Payload (ESP)
- RFC 4543: The Use of Galois Message Authentication Code (GMAC) in IPsec ESP and AH
- RFC 5288: AES Galois Counter Mode (GCM) Cipher Suites for TLS
- RFC 6367: Addition of the Camellia Cipher Suites to Transport Layer Security (TLS)
- IEEE 802.1AE – Media Access Control (MAC) Security
- IEEE Security in Storage Working Group developed the P1619.1 standard
- INCITS T11 Technical Committee works on Fibre Channel – Security Protocols project.
- AES-GCM and AES-CCM Authenticated Encryption in Secure RTP (SRTP)






![{\displaystyle {\begin{aligned}X_{i}^{'}&={\begin{cases}0&{\text{for }}i\leq 0\\\left(X_{i-k}^{'}\oplus S_{i}\right)\cdot H^{k}&{\text{for }}i=1,\ldots ,m+n+1-k\\\end{cases}}\\[6pt]X_{i}&=\sum _{j=1}^{k}\left(X_{i+j-2k}^{'}\oplus S_{i+j-k}\right)\cdot H^{k-j+1}\end{aligned}}}](https://wikimedia.riteme.site/api/rest_v1/media/math/render/svg/72990f43f2b63e67e563b023688b6bea1e42898f)
