Jump to content

File:Riemann sphere1.jpg

Page contents not supported in other languages.
This is a file from the Wikimedia Commons
From Wikipedia, the free encyclopedia

Original file (1,280 × 1,024 pixels, file size: 215 KB, MIME type: image/jpeg)

File:Riemann sphere1.svg is a vector version of this file. It should be used in place of this JPG file when not inferior.
File:Riemann sphere1.jpg → File:Riemann sphere1.svg
For more information, see Help:SVG.
In other languages
Alemannisch ∙ Bahasa Indonesia ∙ Bahasa Melayu ∙ British English ∙ català ∙ čeština ∙ dansk ∙ Deutsch ∙ eesti ∙ English ∙ español ∙ Esperanto ∙ euskara ∙ français ∙ Frysk ∙ galego ∙ hrvatski ∙ Ido ∙ italiano ∙ lietuvių ∙ magyar ∙ Nederlands ∙ norsk bokmål ∙ norsk nynorsk ∙ occitan ∙ Plattdüütsch ∙ polski ∙ português ∙ português do Brasil ∙ română ∙ Scots ∙ sicilianu ∙ slovenčina ∙ slovenščina ∙ suomi ∙ svenska ∙ Tiếng Việt ∙ Türkçe ∙ vèneto ∙ Ελληνικά ∙ беларуская (тарашкевіца) ∙ български ∙ македонски ∙ нохчийн ∙ русский ∙ српски / srpski ∙ татарча/tatarça ∙ українська ∙ ქართული ∙ հայերեն ∙ বাংলা ∙ தமிழ் ∙ മലയാളം ∙ ไทย ∙ 한국어 ∙ 日本語 ∙ 简体中文 ∙ 繁體中文 ∙ עברית ∙ العربية ∙ فارسی ∙ +/−
New SVG image

This image was uploaded in the JPEG format even though it consists of non-photographic data. This information could be stored more efficiently or accurately in the PNG or SVG format. If possible, please upload a PNG or SVG version of this image without compression artifacts, derived from a non-JPEG source (or with existing artifacts removed). After doing so, please tag the JPEG version with {{Superseded|NewImage.ext}} and remove this tag. This tag should not be applied to photographs or scans. If this image is a diagram or other image suitable for vectorisation, please tag this image with {{Convert to SVG}} instead of {{BadJPEG}}. If not suitable for vectorisation, use {{Convert to PNG}}. For more information, see {{BadJPEG}}.

Summary

Description

Sphère de Riemann, démonstration de la projection

English: rendering of the graph of the Sphere of Rieman
Source Own work. Merci à Friedrich A. Lohmüller pour sa bibliothèque POV.
Author Jean-Christophe BENOIST 


//------------------------------------------------------------------------
#version 3.6;
global_settings {  assumed_gamma 1 }
//------------------------------------------------------------------------
#include "colors.inc"
#include "textures.inc"
#include "glass.inc"
#include "metals.inc"
#include "golds.inc"
#include "stones.inc"
#include "woods.inc"
#include "shapes.inc"
#include "shapes2.inc"
#include "functions.inc"
#include "math.inc"          
#include "transforms.inc"
//------------------------------------------------------------------------
#declare Camera_0 = camera {                                 // xy-view
                             angle 20
                             location  <8.0 , 8.0 ,-24.0>
                             right     x*image_width/image_height
                             look_at   <1 , 0 , 0>
                           }

#declare Camera_1 = camera {                                // diagonal view
                             angle 9
                             location  <15.0 ,15 ,-60.0>
                             right     x*image_width/image_height
                             look_at   <1 , 0 , 0>
                           }
#declare Camera_2 = camera {                               // yz-view
                             angle 20          
                             location  <31.0 , 7.0 ,1.0>
                             right     x*image_width/image_height
                             look_at   <0 , 0 , 0>
                           }
#declare Camera_3 = camera { 
                             angle 20
                             location  < 0.0 , 37.5 ,-0.0001>
                             right     x*image_width/image_height
                             look_at   <0 , 0 , 0>
                           }

camera{Camera_0}

//------------------------------------------------------------------------
// sun -------------------------------------------------------------------
light_source{<3000,5500,-1000> color White }
// sky -------------------------------------------------------------------
sky_sphere{ pigment{ gradient <0,1,0>
                     color_map{ [0   color rgb<1,1,1>         ]//White
                                [0.4 color rgb<1,1,1>]  //~Navy
                                [0.6 color rgb<1,1,1>]  //<0.14,0.14,0.56>]//~Navy
                                [1.0 color rgb<1,1,1>         ]//White
                              }
                     scale 2 }
           } // end of sky_sphere 
//------------------------------------------------------------------------
                                                                    
                                                                    
                                                                    
                                                                    
                                                                    
                                                                    
//------------------------------ the Axes --------------------------------
//------------------------------------------------------------------------
#macro Axis_( AxisLen, Dark_Texture,Light_Texture) 
 union{
    cylinder { <0,-AxisLen-3,0>,<0,AxisLen,0>,0.017
               texture{checker texture{Dark_Texture } 
                               texture{Light_Texture}
                       translate<0.1,0,0.1>}
             }
    cone{<0,AxisLen,0>,0.1,<0,AxisLen+0.3,0>,0
          texture{Dark_Texture}
         }
     } // end of union                   
#end // of macro "Axis()"
//------------------------------------------------------------------------
#macro AxisXYZ( AxisLenX, AxisLenY, AxisLenZ, Tex_Dark, Tex_Light)
//--------------------- drawing of 3 Axes --------------------------------
union{
#if (AxisLenX != 0)
 object { Axis_(AxisLenX, Tex_Dark, Tex_Light)   rotate< 0,0,-90>}// x-Axis
 text   { ttf "arial.ttf",  " ",  0.15,  0  texture{Tex_Dark} 
          scale 0.5 translate <AxisLenX+0.05,0.4,-0.10>}
#end // of #if 
#if (AxisLenY != 0)
 object { Axis_(AxisLenY, Tex_Dark, Tex_Light)   rotate< 0,0,  0>}// y-Axis
 text   { ttf "arial.ttf",  "z",  0.15,  0  texture{Tex_Dark}    
           scale 0.5 translate <-0.55,AxisLenY+0.20,-0.10>}
#end // of #if 
#if (AxisLenZ != 0)
 object { Axis_(AxisLenZ, Tex_Dark, Tex_Light)   rotate<90,0,  0>}// z-Axis
 text   { ttf "arial.ttf",  " ",  0.15,  0  texture{Tex_Dark}
               scale 0.5 translate <-0.55,0.1,AxisLenZ+0.10>}
#end // of #if 
} // end of union
#end// of macro "AxisXYZ( ... )"
//------------------------------------------------------------------------

#declare Texture_A_Dark  = texture {
                               pigment{color rgb<0.5,0.5,0.5>}
                               finish {ambient 0.15 diffuse 0.85 phong 1}
                             }
#declare Texture_A_Light = texture { 
                               pigment{color rgb<1,1,1>}
                               finish {ambient 0.15 diffuse 0.85 phong 1}
                             }
                                                                                                              
                                                                    
                                                                    
                                                                    
                                                                    
                                                                    
                                                                    
                                                                                                              
                                                                                                              
object{ AxisXYZ( 25.0, 0, 25.0, Texture_A_Dark, Texture_A_Dark)} // <<<<<<<<<<<<<<<<< adapt the axes here !!!


#declare        TextScale=0.5;

//-------------------------------------------------- end of coordinate axes


// ground -----------------------------------------------------------------
//---------------------------------<<< settings of squered plane dimensions
#declare RasterScale = 2.0/2;
#declare RasterHalfLine  = 0.03/4;  
#declare RasterHalfLineZ = 0.03/2; 
//-------------------------------------------------------------------------
#macro Raster(RScale, HLine) 
       pigment{ gradient x scale RScale
                color_map{[0.000   color rgbt<1,1,1,1>*0.2]
                          [0+HLine color rgbt<1,1,1,1>*0.2]
                          [0+HLine color rgbt<1,1,1,1>]
                          [1-HLine color rgbt<1,1,1,1>]
                          [1-HLine color rgbt<1,1,1,1>*0.2]
                          [1.000   color rgbt<1,1,1,1>*0.2]} }
       finish { ambient 0.15 diffuse 0.85}
 #end// of Raster(RScale, HLine)-macro    
//-------------------------------------------------------------------------
    

plane { <0,1,0>, 0    // plane with layered textures
        texture { pigment{color rgbt<1,1,1,0.7>*1.1}
                  finish {ambient 0.45 diffuse 0.85}}
        texture { Raster(RasterScale,RasterHalfLine ) rotate<0,0,0> }
        texture { Raster(RasterScale,RasterHalfLineZ) rotate<0,90,0>}
        rotate<0,0,0>
        no_shadow
      }
//------------------------------------------------ end of squered plane XZ   



// 
//------------------------------------------------------------------------------------
#include "analytical_g.inc" 





//--------------------------------------------------------------------------
//---------------------------- objects in scene ----------------------------
//--------------------------------------------------------------------------
#default{ finish {ambient 0.15 diffuse 0.85} } // 



//-----------------------------------------------------------------------------------
#declare Rl  = 0.035; // radius of lines  - Radius der Strecken 
#declare Rp  = 0.06; // radius of points - Radius der Punkte 


//------------------------------------------------------------------------------------
// ----------------------------------------------------------------------------------- 

// ----------------------------------------------------------------------------------- 
// ---------------------  Punti e Vettori  - Punkte und Vektoren -  Points and Vectors
//------------------------------------------------------------------------------------

#declare M1 = < 0, 0.0,0.0>;  
#declare R1  = 3;   

#declare M2  = < 0.0,0.0, 0.0>;
#declare Rx  = 3.00;
#declare Ry  = 1.00;
#declare Rz  = 2.00;

#declare P1   = < 3, 0, 0>;
#declare Pi   = < 0, 0, 3>;
#declare PPinf = < 0, 3, 0>;        
#declare PP0   = < 0, -3, 0>;  
#declare P0   = <0,0,0>;

sphere{ P1, Rp  pigment{color YellowGreen}}
text { ttf "arial.ttf", "1",0.1,0 
       scale TextScale rotate<0,0,0> translate P1+<0.2,0.1,-0.2> pigment{ color Red } no_shadow}


sphere{ Pi, Rp  pigment{color YellowGreen}}
text { ttf "arial.ttf", "i",0.1,0 
       scale TextScale rotate<0,0,0> translate Pi+<-0.1,0.1,0.2> pigment{ color Red } no_shadow}
       
       
sphere{ PPinf, Rp  pigment{color YellowGreen}}
text { ttf "Mathematica1.ttf", concat("R(",chr(165),")"),0.1,0 
       scale TextScale rotate<0,0,0> translate PPinf+<-0.1,0.1,0> pigment{ color Red } no_shadow}             
       
       
sphere{ PP0, Rp  pigment{color YellowGreen}}
text { ttf "Mathematica1.ttf", "R(0)",-0.1,0 
       scale TextScale rotate<0,0,0> translate PP0+<-0.1,0.1,0> pigment{ color Red } no_shadow}         
       
sphere{ P0, Rp  pigment{color YellowGreen}}
text { ttf "Mathematica1.ttf", "0",-0.1,0 
       scale TextScale rotate<0,0,0> translate P0+<-0.1,0.1,0> pigment{ color Red } no_shadow}           
 
 
//object{ Show_Yxz( M1, Rl/2) pigment{ color Yellow }}
//object{ Show_Yxz( M2, Rl/2) pigment{ color Yellow }}
//------------------------------------------------------------------------------------
// --------------------------------------------------------------- Zeichnen ---------- 
// ---------------------------------------------------------------- Drawing ---------- 

                               
#declare RSphere=
object {
        sphere{ M1, R1                          pigment{ color Yellow transmit 0.6 } finish {phong 0.3}}
}                               
                               
                               
#declare PPlan1 = <4.5,0,0>;     
               
object{ Vector (PPinf, PPlan1, Rl)
         pigment{color Red}}  

sphere{ PPlan1, Rp  pigment{color Green}}          
object{ Show_Yxz( PPlan1, Rl/2)
        pigment{ color Orange }}
text { ttf "arial.ttf", "A",0.1,0 
       scale TextScale rotate<0,0,0> translate PPlan1+<0.1,0.0,-0.4> pigment{ color Red } no_shadow}        

// point of intersection 
#declare Hit_the_Object =  trace ( RSphere, PPinf, PPlan1 - PPinf );                      

sphere{ Hit_the_Object, Rp  pigment{color Green}}
text { ttf "Mathematica1.ttf", "a=R(A)",0.1,0 
       scale TextScale rotate<0,0,0> translate Hit_the_Object+<0.2,0.0,-0.2> pigment{ color Red } no_shadow}  
                 






#declare PPlan2 = <-1.5,0,0>;     
               


sphere{ PPlan2, Rp  pigment{color Green}}          
object{ Show_Yxz( PPlan2, Rl/2)
        pigment{ color Orange }}
text { ttf "arial.ttf", "B",0.1,0 
       scale TextScale rotate<0,0,0> translate PPlan2+<0.3,0.0,-0.4> pigment{ color Red } no_shadow}        

// point of intersection 
#declare Hit_the_Object =  trace ( RSphere, PPinf, PPlan2 - PPinf );   

object{ Vector (PPinf, Hit_the_Object, Rl)
         pigment{color Red}}                     

sphere{ Hit_the_Object, Rp  pigment{color Green}}
text { ttf "Mathematica1.ttf", "b=R(B)",0.1,0 
       scale TextScale rotate<0,0,0> translate Hit_the_Object+<0.2,0.0,-0.2> pigment{ color Red } no_shadow}  



                 
                 
                 
object {RSphere}

Licensing

I, the copyright holder of this work, hereby publish it under the following licenses:
GNU head Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled GNU Free Documentation License.
w:en:Creative Commons
attribution share alike 		This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license.
You are free:
  • to share – to copy, distribute and transmit the work
  • to remix – to adapt the work
Under the following conditions:
  • attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
  • share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.
This licensing tag was added to this file as part of the GFDL licensing update.
w:en:Creative Commons
attribution share alike
This file is licensed under the Creative Commons Attribution-Share Alike 2.5 Generic, 2.0 Generic and 1.0 Generic license.
You are free:
  • to share – to copy, distribute and transmit the work
  • to remix – to adapt the work
Under the following conditions:
  • attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
  • share alike – If you remix, transform, or build upon the material, you must distribute your contributions under the same or compatible license as the original.
You may select the license of your choice.

Captions

Add a one-line explanation of what this file represents

Items portrayed in this file

depicts

File history

Click on a date/time to view the file as it appeared at that time.

Date/TimeThumbnailDimensionsUserComment
current16:11, 4 June 2007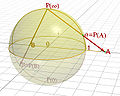Thumbnail for version as of 16:11, 4 June 20071,280 × 1,024 (215 KB)Jean-Christophe BENOIST== Description == {{Information |Description=Sphère de Riemann, démonstration de la projection |Source=Oeuvre personnelle. Merci à Friedrich A. Lohmüller pour sa bibliothèque POV. |Date= |Author=[[:fr:User:Jean-Christophe BENOIST|Jean-Christophe BENO
15:39, 4 June 2007Thumbnail for version as of 15:39, 4 June 20071,280 × 1,024 (215 KB)Jean-Christophe BENOIST== Description == {{Information |Description=Sphère de Riemann, démonstration de la projection |Source=Oeuvre personnelle. Merci à Friedrich A. Lohmüller pour sa bibliothèque POV. |Date= |Author=[[:fr:User:Jean-Christophe BENOIST|Jean-Christophe BENO
06:08, 4 June 2007Thumbnail for version as of 06:08, 4 June 20071,280 × 1,024 (179 KB)Jean-Christophe BENOIST== Description == {{Information |Description=Sphère de Riemann, démonstration de la projection |Source=Oeuvre personnelle. Merci à Friedrich A. Lohmüller pour sa bibliothèque POV. |Date= |Author=[[:fr:User:Jean-Christophe BENOIST|Jean-Christophe BENO
23:47, 3 June 2007Thumbnail for version as of 23:47, 3 June 20071,280 × 1,024 (175 KB)Jean-Christophe BENOIST== Description == {{Information |Description=Sphère de Riemann, démonstration de la projection |Source=Oeuvre personnelle. Merci à Friedrich A. Lohmüller pour sa bibliothèque POV. |Date= |Author=[[:fr:User:Jean-Christophe BENOIST|Jean-Christophe BENO

The following page uses this file:

Global file usage

The following other wikis use this file:

Metadata

This file contains additional information, probably added from the digital camera or scanner used to create or digitize it.

If the file has been modified from its original state, some details may not fully reflect the modified file.

Retrieved from "https://wiki.riteme.site/wiki/File:Riemann_sphere1.jpg"