Fourier-transform infrared spectroscopy
Fourier transform infrared spectroscopy (FTIR)[1] is a technique used to obtain an infrared spectrum of absorption or emission of a solid, liquid, or gas. An FTIR spectrometer simultaneously collects high-resolution spectral data over a wide spectral range. This confers a significant advantage over a dispersive spectrometer, which measures intensity over a narrow range of wavelengths at a time.
The term Fourier transform infrared spectroscopy originates from the fact that a Fourier transform (a mathematical process) is required to convert the raw data into the actual spectrum.

Conceptual introduction
[edit]This section needs additional citations for verification. (June 2022) |
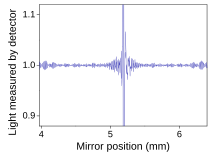
The goal of absorption spectroscopy techniques (FTIR, ultraviolet-visible ("UV-vis") spectroscopy, etc.) is to measure how much light a sample absorbs at each wavelength.[2] The most straightforward way to do this, the "dispersive spectroscopy" technique, is to shine a monochromatic light beam at a sample, measure how much of the light is absorbed, and repeat for each different wavelength. (This is how some UV–vis spectrometers work, for example.)
Fourier transform spectroscopy is a less intuitive way to obtain the same information. Rather than shining a monochromatic beam of light (a beam composed of only a single wavelength) at the sample, this technique shines a beam containing many frequencies of light at once and measures how much of that beam is absorbed by the sample. Next, the beam is modified to contain a different combination of frequencies, giving a second data point. This process is rapidly repeated many times over a short time span. Afterwards, a computer takes all this data and works backward to infer what the absorption is at each wavelength.[2]
The beam described above is generated by starting with a broadband light source—one containing the full spectrum of wavelengths to be measured. The light shines into a Michelson interferometer—a certain configuration of mirrors, one of which is moved by a motor. As this mirror moves, each wavelength of light in the beam is periodically blocked, transmitted, blocked, transmitted, by the interferometer, due to wave interference. Different wavelengths are modulated at different rates, so that at each moment or mirror position the beam coming out of the interferometer has a different spectrum.[2]
As mentioned, computer processing is required to turn the raw data (light absorption for each mirror position) into the desired result (light absorption for each wavelength).[2] The processing required turns out to be a common algorithm called the Fourier transform. The Fourier transform converts one domain (in this case displacement of the mirror in cm) into its inverse domain (wavenumbers in cm−1). The raw data is called an "interferogram".
History
[edit]The first low-cost spectrophotometer capable of recording an infrared spectrum was the Perkin-Elmer Infracord produced in 1957.[3] This instrument covered the wavelength range from 2.5 μm to 15 μm (wavenumber range 4,000 cm−1 to 660 cm−1). The lower wavelength limit was chosen to encompass the highest known vibration frequency due to a fundamental molecular vibration. The upper limit was imposed by the fact that the dispersing element was a prism made from a single crystal of rock-salt (sodium chloride), which becomes opaque at wavelengths longer than about 15 μm; this spectral region became known as the rock-salt region. Later instruments used potassium bromide prisms to extend the range to 25 μm (400 cm−1) and caesium iodide 50 μm (200 cm−1). The region beyond 50 μm (200 cm−1) became known as the far-infrared region; at very long wavelengths it merges into the microwave region. Measurements in the far infrared needed the development of accurately ruled diffraction gratings to replace the prisms as dispersing elements, since salt crystals are opaque in this region. More sensitive detectors than the bolometer were required because of the low energy of the radiation. One such was the Golay detector. An additional issue is the need to exclude atmospheric water vapour because water vapour has an intense pure rotational spectrum in this region. Far-infrared spectrophotometers were cumbersome, slow and expensive. The advantages of the Michelson interferometer were well-known, but considerable technical difficulties had to be overcome before a commercial instrument could be built. Also an electronic computer was needed to perform the required Fourier transform, and this only became practicable with the advent of minicomputers, such as the PDP-8, which became available in 1965. Digilab pioneered the world's first commercial FTIR spectrometer (Model FTS-14) in 1969.[1] Digilab FTIRs are now a part of Agilent Technologies's molecular product line after Agilent acquired spectroscopy business from Varian.[4][5]
Michelson interferometer
[edit]This section needs additional citations for verification. (June 2022) |

In a Michelson interferometer adapted for FTIR, light from the polychromatic infrared source, approximately a black-body radiator, is collimated and directed to a beam splitter. Ideally 50% of the light is refracted towards the fixed mirror and 50% is transmitted towards the moving mirror. Light is reflected from the two mirrors back to the beam splitter and some fraction of the original light passes into the sample compartment. There, the light is focused on the sample. On leaving the sample compartment the light is refocused on to the detector. The difference in optical path length between the two arms to the interferometer is known as the retardation or optical path difference (OPD). An interferogram is obtained by varying the retardation and recording the signal from the detector for various values of the retardation. The form of the interferogram when no sample is present depends on factors such as the variation of source intensity and splitter efficiency with wavelength. This results in a maximum at zero retardation, when there is constructive interference at all wavelengths, followed by series of "wiggles". The position of zero retardation is determined accurately by finding the point of maximum intensity in the interferogram. When a sample is present the background interferogram is modulated by the presence of absorption bands in the sample.[2]
Commercial spectrometers use Michelson interferometers with a variety of scanning mechanisms to generate the path difference. Common to all these arrangements is the need to ensure that the two beams recombine exactly as the system scans. The simplest systems have a plane mirror that moves linearly to vary the path of one beam. In this arrangement the moving mirror must not tilt or wobble as this would affect how the beams overlap as they recombine. Some systems incorporate a compensating mechanism that automatically adjusts the orientation of one mirror to maintain the alignment. Arrangements that avoid this problem include using cube corner reflectors instead of plane mirrors as these have the property of returning any incident beam in a parallel direction regardless of orientation.

Systems where the path difference is generated by a rotary movement have proved very successful. One common system incorporates a pair of parallel mirrors in one beam that can be rotated to vary the path without displacing the returning beam. Another is the double pendulum design where the path in one arm of the interferometer increases as the path in the other decreases.
A quite different approach involves moving a wedge of an IR-transparent material such as KBr into one of the beams. Increasing the thickness of KBr in the beam increases the optical path because the refractive index is higher than that of air. One limitation of this approach is that the variation of refractive index over the wavelength range limits the accuracy of the wavelength calibration.
Measuring and processing the interferogram
[edit]The interferogram has to be measured from zero path difference to a maximum length that depends on the resolution required. In practice the scan can be on either side of zero resulting in a double-sided interferogram. Mechanical design limitations may mean that for the highest resolution the scan runs to the maximum OPD on one side of zero only.
The interferogram is converted to a spectrum by Fourier transformation. This requires it to be stored in digital form as a series of values at equal intervals of the path difference between the two beams. To measure the path difference a laser beam is sent through the interferometer, generating a sinusoidal signal where the separation between successive maxima is equal to the wavelength of the laser (typically a 633 nm HeNe laser is used). This can trigger an analog-to-digital converter to measure the IR signal each time the laser signal passes through zero. Alternatively, the laser and IR signals can be measured synchronously at smaller intervals with the IR signal at points corresponding to the laser signal zero crossing being determined by interpolation.[6] This approach allows the use of analog-to-digital converters that are more accurate and precise than converters that can be triggered, resulting in lower noise.

The result of Fourier transformation is a spectrum of the signal at a series of discrete wavelengths. The range of wavelengths that can be used in the calculation is limited by the separation of the data points in the interferogram. The shortest wavelength that can be recognized is twice the separation between these data points. For example, with one point per wavelength of a HeNe reference laser at 0.633 μm (15800 cm−1) the shortest wavelength would be 1.266 μm (7900 cm−1). Because of aliasing, any energy at shorter wavelengths would be interpreted as coming from longer wavelengths and so has to be minimized optically or electronically. The spectral resolution, i.e. the separation between wavelengths that can be distinguished, is determined by the maximum OPD. The wavelengths used in calculating the Fourier transform are such that an exact number of wavelengths fit into the length of the interferogram from zero to the maximum OPD as this makes their contributions orthogonal. This results in a spectrum with points separated by equal frequency intervals.
For a maximum path difference d adjacent wavelengths λ1 and λ2 will have n and (n+1) cycles, respectively, in the interferogram. The corresponding frequencies are ν1 and ν2:
d = nλ1 and d = (n+1)λ2 λ1 = d/n and λ2 =d/(n+1) ν1 = 1/λ1 and ν2 = 1/λ2 ν1 = n/d and ν2 = (n+1)/d ν2 − ν1 = 1/d
The separation is the inverse of the maximum OPD. For example, a maximum OPD of 2 cm results in a separation of 0.5 cm−1. This is the spectral resolution in the sense that the value at one point is independent of the values at adjacent points. Most instruments can be operated at different resolutions by choosing different OPD's. Instruments for routine analyses typically have a best resolution of around 0.5 cm−1, while spectrometers have been built with resolutions as high as 0.001 cm−1, corresponding to a maximum OPD of 10 m. The point in the interferogram corresponding to zero path difference has to be identified, commonly by assuming it is where the maximum signal occurs. This so-called centerburst is not always symmetrical in real world spectrometers so a phase correction may have to be calculated. The interferogram signal decays as the path difference increases, the rate of decay being inversely related to the width of features in the spectrum. If the OPD is not large enough to allow the interferogram signal to decay to a negligible level there will be unwanted oscillations or sidelobes associated with the features in the resulting spectrum. To reduce these sidelobes the interferogram is usually multiplied by a function that approaches zero at the maximum OPD. This so-called apodization reduces the amplitude of any sidelobes and also the noise level at the expense of some reduction in resolution.
For rapid calculation the number of points in the interferogram has to equal a power of two. A string of zeroes may be added to the measured interferogram to achieve this. More zeroes may be added in a process called zero filling to improve the appearance of the final spectrum although there is no improvement in resolution. Alternatively, interpolation after the Fourier transform gives a similar result.[citation needed]
Advantages
[edit]There are three principal advantages for an FT spectrometer compared to a scanning (dispersive) spectrometer.[1]
- The multiplex or Fellgett's advantage (named after Peter Fellgett). This arises from the fact that information from all wavelengths is collected simultaneously. It results in a higher signal-to-noise ratio for a given scan-time for observations limited by a fixed detector noise contribution (typically in the thermal infrared spectral region where a photodetector is limited by generation-recombination noise). For a spectrum with m resolution elements, this increase is equal to the square root of m. Alternatively, it allows a shorter scan-time for a given resolution. In practice multiple scans are often averaged, increasing the signal-to-noise ratio by the square root of the number of scans.
- The throughput or Jacquinot's advantage (named after Pierre Jacquinot). This results from the fact that in a dispersive instrument, the monochromator has entrance and exit slits which restrict the amount of light that passes through it. The interferometer throughput is determined only by the diameter of the collimated beam coming from the source. Although no slits are needed, FTIR spectrometers do require an aperture to restrict the convergence of the collimated beam in the interferometer. This is because convergent rays are modulated at different frequencies as the path difference is varied. Such an aperture is called a Jacquinot stop.[1] For a given resolution and wavelength this circular aperture allows more light through than a slit, resulting in a higher signal-to-noise ratio.
- The wavelength accuracy or Connes' advantage (named after Janine Connes). The wavelength scale is calibrated by a laser beam of known wavelength that passes through the interferometer. This is much more stable and accurate than in dispersive instruments where the scale depends on the mechanical movement of diffraction gratings. In practice, the accuracy is limited by the divergence of the beam in the interferometer which depends on the resolution.
Another minor advantage is less sensitivity to stray light, that is radiation of one wavelength appearing at another wavelength in the spectrum. In dispersive instruments, this is the result of imperfections in the diffraction gratings and accidental reflections. In FT instruments there is no direct equivalent as the apparent wavelength is determined by the modulation frequency in the interferometer.
Resolution
[edit]The interferogram belongs in the length dimension. Fourier transform (FT) inverts the dimension, so the FT of the interferogram belongs in the reciprocal length dimension([L−1]), that is the dimension of wavenumber. The spectral resolution in cm−1 is equal to the reciprocal of the maximal retardation in cm. Thus a 4 cm−1 resolution will be obtained if the maximal retardation is 0.25 cm; this is typical of the cheaper FTIR instruments. Much higher resolution can be obtained by increasing the maximal retardation. This is not easy, as the moving mirror must travel in a near-perfect straight line. The use of corner-cube mirrors in place of the flat mirrors is helpful, as an outgoing ray from a corner-cube mirror is parallel to the incoming ray, regardless of the orientation of the mirror about axes perpendicular to the axis of the light beam.
A spectrometer with 0.001 cm−1 resolution is now available commercially. The throughput advantage is important for high-resolution FTIR, as the monochromator in a dispersive instrument with the same resolution would have very narrow entrance and exit slits.
In 1966 Janine Connes measured the temperature of the atmosphere of Venus by recording the vibration-rotation spectrum of Venusian CO2 at 0.1 cm−1 resolution.[7] Michelson himself attempted to resolve the hydrogen Hα emission band in the spectrum of a hydrogen atom into its two components by using his interferometer.[1] p25
Motivation
[edit]FTIR is a method of measuring infrared absorption and emission spectra. For a discussion of why people measure infrared absorption and emission spectra, i.e. why and how substances absorb and emit infrared light, see the article: Infrared spectroscopy.
Components
[edit]
IR sources
[edit]FTIR spectrometers are mostly used for measurements in the mid and near IR regions. For the mid-IR region, 2−25 μm (5,000–400 cm−1), the most common source is a silicon carbide (SiC) element heated to about 1,200 K (930 °C; 1,700 °F) (Globar). The output is similar to a blackbody. Shorter wavelengths of the near-IR, 1−2.5 μm (10,000–4,000 cm−1), require a higher temperature source, typically a tungsten-halogen lamp. The long wavelength output of these is limited to about 5 μm (2,000 cm−1) by the absorption of the quartz envelope. For the far-IR, especially at wavelengths beyond 50 μm (200 cm−1) a mercury discharge lamp gives higher output than a thermal source.[8]
Detectors
[edit]Far-IR spectrometers commonly use pyroelectric detectors that respond to changes in temperature as the intensity of IR radiation falling on them varies. The sensitive elements in these detectors are either deuterated triglycine sulfate (DTGS) or lithium tantalate (LiTaO3). These detectors operate at ambient temperatures and provide adequate sensitivity for most routine applications. To achieve the best sensitivity the time for a scan is typically a few seconds. Cooled photoelectric detectors are employed for situations requiring higher sensitivity or faster response. Liquid nitrogen cooled mercury cadmium telluride (MCT) detectors are the most widely used in the mid-IR. With these detectors an interferogram can be measured in as little as 10 milliseconds. Uncooled indium gallium arsenide photodiodes or DTGS are the usual choices in near-IR systems. Very sensitive liquid-helium-cooled silicon or germanium bolometers are used in the far-IR where both sources and beamsplitters are inefficient.[citation needed]
Beam splitter
[edit]
An ideal beam-splitter transmits and reflects 50% of the incident radiation. However, as any material has a limited range of optical transmittance, several beam-splitters may be used interchangeably to cover a wide spectral range.
In a simple Michelson interferometer, one beam passes twice through the beamsplitter but the other passes through only once. To correct for this, an additional compensator plate of equal thickness is incorporated.
For the mid-IR region, the beamsplitter is usually made of KBr with a germanium-based coating that makes it semi-reflective. KBr absorbs strongly at wavelengths beyond 25 μm (400 cm−1), so CsI or KRS-5 are sometimes used to extend the range to about 50 μm (200 cm−1). ZnSe is an alternative where moisture vapour can be a problem, but is limited to about 20 μm (500 cm−1).
CaF2 is the usual material for the near-IR, being both harder and less sensitive to moisture than KBr, but cannot be used beyond about 8 μm (1,200 cm−1).
Far-IR beamsplitters are mostly based on polymer films, and cover a limited wavelength range.[9]
Attenuated total reflectance
[edit]Attenuated total reflectance (ATR) is one accessory of FTIR spectrophotometer to measure surface properties of solid or thin film samples rather than their bulk properties. Generally, ATR has a penetration depth of around 1 or 2 micrometers depending on sample conditions.
Fourier transform
[edit]The interferogram in practice consists of a set of intensities measured for discrete values of retardation. The difference between successive retardation values is constant. Thus, a discrete Fourier transform is needed. The fast Fourier transform (FFT) algorithm is used.
Spectral range
[edit]Far-infrared
[edit]The first FTIR spectrometers were developed for far-infrared range. The reason for this has to do with the mechanical tolerance needed for good optical performance, which is related to the wavelength of the light being used. For the relatively long wavelengths of the far infrared, ~10 μm tolerances are adequate, whereas for the rock-salt region tolerances have to be better than 1 μm. A typical instrument was the cube interferometer developed at the NPL[10] and marketed by Grubb Parsons. It used a stepper motor to drive the moving mirror, recording the detector response after each step was completed.
Mid-infrared
[edit]With the advent of cheap microcomputers it became possible to have a computer dedicated to controlling the spectrometer, collecting the data, doing the Fourier transform and presenting the spectrum. This provided the impetus for the development of FTIR spectrometers for the rock-salt region. The problems of manufacturing ultra-high precision optical and mechanical components had to be solved. A wide range of instruments are now available commercially. Although instrument design has become more sophisticated, the basic principles remain the same. Nowadays, the moving mirror of the interferometer moves at a constant velocity, and sampling of the interferogram is triggered by finding zero-crossings in the fringes of a secondary interferometer lit by a helium–neon laser. In modern FTIR systems the constant mirror velocity is not strictly required, as long as the laser fringes and the original interferogram are recorded simultaneously with higher sampling rate and then re-interpolated on a constant grid, as pioneered by James W. Brault. This confers very high wavenumber accuracy on the resulting infrared spectrum and avoids wavenumber calibration errors.
Near-infrared
[edit]The near-infrared region spans the wavelength range between the rock-salt region and the start of the visible region at about 750 nm. Overtones of fundamental vibrations can be observed in this region. It is used mainly in industrial applications such as process control and chemical imaging.
Applications
[edit]FTIR can be used in all applications where a dispersive spectrometer was used in the past (see external links). In addition, the improved sensitivity and speed have opened up new areas of application. Spectra can be measured in situations where very little energy reaches the detector. Fourier transform infrared spectroscopy is used in geology,[11] chemistry, materials, botany[12] and biology research fields.[13]
Nano and biological materials
[edit]FTIR is also used to investigate various nanomaterials and proteins in hydrophobic membrane environments. Studies show the ability of FTIR to directly determine the polarity at a given site along the backbone of a transmembrane protein.[14][15] The bond features involved with various organic and inorganic nanomaterials and their quantitative analysis can be done with the help of FTIR.[16][17]
Microscopy and imaging
[edit]An infrared microscope allows samples to be observed and spectra measured from regions as small as 5 microns across. Images can be generated by combining a microscope with linear or 2-D array detectors. The spatial resolution can approach 5 microns with tens of thousands of pixels. The images contain a spectrum for each pixel and can be viewed as maps showing the intensity at any wavelength or combination of wavelengths. This allows the distribution of different chemical species within the sample to be seen[citation needed]. This technique has been applied in various biological applications including the analysis of tissue sections as an alternative to conventional histopathology,[citation needed] examining the homogeneity of pharmaceutical tablets[citation needed], and for differentiating morphologically-similar pollen grains.[18]
Nanoscale and spectroscopy below the diffraction limit
[edit]The spatial resolution of FTIR can be further improved below the micrometer scale by integrating it into scanning near-field optical microscopy platform. The corresponding technique is called nano-FTIR and allows for performing broadband spectroscopy on materials in ultra-small quantities (single viruses and protein complexes) and with 10 to 20 nm spatial resolution.[19]
FTIR as detector in chromatography
[edit]The speed of FTIR allows spectra to be obtained from compounds as they are separated by a gas chromatograph. However this technique is little used compared to GC-MS (gas chromatography-mass spectrometry) which is more sensitive. The GC-IR method is particularly useful for identifying isomers, which by their nature have identical masses. Liquid chromatography fractions are more difficult because of the solvent present. One notable exception is to measure chain branching as a function of molecular size in polyethylene using gel permeation chromatography, which is possible using chlorinated solvents that have no absorption in the area in question.
TG-IR (thermogravimetric analysis-infrared spectrometry)
[edit]Measuring the gas evolved as a material is heated allows qualitative identification of the species to complement the purely quantitative information provided by measuring the weight loss.
Water content determination in plastics and composites
[edit]FTIR analysis is used to determine water content in fairly thin plastic and composite parts, more commonly in the laboratory setting. Such FTIR methods have long been used for plastics, and became extended for composite materials in 2018, when the method was introduced by Krauklis, Gagani and Echtermeyer.[20] FTIR method uses the maxima of the absorbance band at about 5,200 cm−1 which correlates with the true water content in the material.
See also
[edit]- Discrete Fourier transform – Type of Fourier transform in discrete mathematics − for computing periodicity in evenly spaced data
- Fourier transform – Mathematical transform that expresses a function of time as a function of frequency
- Fourier transform spectroscopy – Spectroscopy based on time- or space-domain data
- Least-squares spectral analysis – Periodicity computation method − for computing periodicity in unevenly spaced data
References
[edit]- ^ a b c d e Griffiths, P.; de Hasseth, J. A. (18 May 2007). Fourier Transform Infrared Spectrometry (2nd ed.). Wiley-Blackwell. ISBN 978-0-471-19404-0.
- ^ a b c d e Krishnan, Kannan M. (2021). Principles of materials characterization and metrology (Paperback ed.). New York: Oxford University Press. pp. 173–178. ISBN 978-0-19-883025-2.
- ^ "The Infracord double-beam spectrophotometer". Clinical Science. 16 (2). 1957.
- ^ "Agilent Technologies to acquire Varian, Inc. for $1.5 Billion". Agilent. July 27, 2009. Archived from the original on January 13, 2017. Retrieved March 5, 2013.
- ^ "Agilent Technologies completes acquisition of Varian, Inc., marking historic milestone for two Silicon Valley pioneers". Agilent Technologies, Inc. 2010-05-14. Retrieved 2023-11-04.
- ^ Brault, James W. (1996). "New Approach to high-precision Fourier transform spectrometer design". Applied Optics. 35 (16): 2891–2896. Bibcode:1996ApOpt..35.2891B. doi:10.1364/AO.35.002891. PMID 21085438.
- ^ Connes, J.; Connes, P. (1966). "Near-Infrared Planetary Spectra by Fourier Spectroscopy. I. Instruments and Results". Journal of the Optical Society of America. 56 (7): 896–910. doi:10.1364/JOSA.56.000896.
- ^ Smith, D.R.; Morgan, R.L.; Loewenstein, E.V. (1968). "Comparison of the Radiance of Far-Infrared Sources". J. Opt. Soc. Am. 58 (3): 433–434. doi:10.1364/JOSA.58.000433.
- ^ Griffiths, P.R.; Holmes, C (2002). Handbook of Vibrational Spectroscopy, Vol 1. Chichester: John Wiley and Sons.
- ^ Chamberain, J.; Gibbs, J.E.; Gebbie, H.E. (1969). "The determination of refractive index spectra by fourier spectrometry". Infrared Physics. 9 (4): 189–209. Bibcode:1969InfPh...9..185C. doi:10.1016/0020-0891(69)90023-2.
- ^ Singh, Iqbal (2008-09-01). "Renal geology (quantitative renal stone analysis) by 'Fourier transform infrared spectroscopy'". International Urology and Nephrology. 40 (3): 595–602. doi:10.1007/s11255-007-9327-2. ISSN 1573-2584. PMID 18228157. S2CID 2249696.
- ^ Tsagkaris, A. S.; Bechynska, K.; Ntakoulas, D. D.; Pasias, I. N.; Weller, P.; Proestos, C.; Hajslova, J. (2023-06-01). "Investigating the impact of spectral data pre-processing to assess honey botanical origin through Fourier transform infrared spectroscopy (FTIR)". Journal of Food Composition and Analysis. 119: 105276. doi:10.1016/j.jfca.2023.105276. ISSN 0889-1575. S2CID 257530876.
- ^ Baker, Matthew J.; Trevisan, Júlio; Bassan, Paul; Bhargava, Rohit; Butler, Holly J.; Dorling, Konrad M.; Fielden, Peter R.; Fogarty, Simon W.; Fullwood, Nigel J.; Heys, Kelly A.; Hughes, Caryn; Lasch, Peter; Martin-Hirsch, Pierre L.; Obinaju, Blessing; Sockalingum, Ganesh D. (2014). "Using Fourier transform IR spectroscopy to analyze biological materials". Nature Protocols. 9 (8): 1771–1791. doi:10.1038/nprot.2014.110. ISSN 1750-2799. PMC 4480339. PMID 24992094.
- ^ Manor, Joshua; Feldblum, Esther S.; Arkin, Isaiah T. (2012). "Environment Polarity in Proteins Mapped Noninvasively by FTIR Spectroscopy". The Journal of Physical Chemistry Letters. 3 (7): 939–944. doi:10.1021/jz300150v. PMC 3341589. PMID 22563521.
- ^ Brielle, Esther S.; Arkin, Isaiah T. (2018). "Site-Specific Hydrogen Exchange in a Membrane Environment Analyzed by Infrared Spectroscopy". The Journal of Physical Chemistry Letters. 9 (14): 4059–4065. doi:10.1021/acs.jpclett.8b01675. PMID 29957958. S2CID 49621115.
- ^ "Structural, functional and magnetic ordering modifications in graphene oxide and graphite by 100 MeV gold ion irradiation". Vacuum. 182: 109700. 2020-12-01. doi:10.1016/j.vacuum.2020.109700
- ^ Deepty, M., Ch Srinivas, E. Ranjith Kumar, N. Krisha Mohan, C. L. Prajapat, TV Chandrasekhar Rao, Sher Singh Meena, Amit Kumar Verma, and D. L. Sastry. "XRD, EDX, FTIR and ESR spectroscopic studies of co-precipitated Mn–substituted Zn–ferrite nanoparticles." Ceramics International 45, no. 6 (2019): 8037-8044.https://doi.org/10.1016/j.ceramint.2019.01.029
- ^ Scoble, Laura; Ussher, Simon J.; Fitzsimons, Mark F.; Ansell, Lauren; Craven, Matthew; Fyfe, Ralph M. (2024-02-01). "Optimisation of classification methods to differentiate morphologically-similar pollen grains from FT-IR spectra". Review of Palaeobotany and Palynology. 321: 105041. doi:10.1016/j.revpalbo.2023.105041. ISSN 0034-6667.
- ^ Amenabar, Iban; Poly, Simon; Nuansing, Wiwat; Hubrich, Elmar H.; Govyadinov, Alexander A.; Huth, Florian; Krutokhvostov, Roman; Zhang, Lianbing; Knez, Mato (2013-12-04). "Structural analysis and mapping of individual protein complexes by infrared nanospectroscopy". Nature Communications. 4: 2890. Bibcode:2013NatCo...4.2890A. doi:10.1038/ncomms3890. ISSN 2041-1723. PMC 3863900. PMID 24301518.
- ^ Krauklis, A. E.; Gagani, A. I.; Echtermeyer, A. T. (2018). "Near-Infrared Spectroscopic Method for Monitoring Water Content in Epoxy Resins and Fiber-Reinforced Composites". Materials. 11 (4): 586–599. Bibcode:2018Mate...11..586.. doi:10.3390/ma11040586. PMC 5951470. PMID 29641451.
External links
[edit]- Infracord spectrometer photograph
- The Grubb-Parsons-NPL cube interferometer Spectroscopy, part 2 by Dudley Williams, page 81
- Infrared materials Properties of many salt crystals and useful links.
- University FTIR lab example from the University of Bristol
