Metallic mean

Gold, silver, and bronze ratios within their respective rectangles.

The metallic mean (also metallic ratio, metallic constant, or noble means) of a natural number n is a positive real number, denoted here $S_{n},$ that satisfies the following equivalent characterizations:

• the unique positive real number $x$ such that ${\textstyle x=n+{\frac {1}{x}}}$
• the positive root of the quadratic equation $x^{2}-nx-1=0$
• the number ${\textstyle {\frac {n+{\sqrt {n^{2}+4}}}{2}}}$
• the number whose expression as a continued fraction is

  $[n;n,n,n,n,\dots ]=n+{\cfrac {1}{n+{\cfrac {1}{n+{\cfrac {1}{n+{\cfrac {1}{n+\ddots \,}}}}}}}}$

Metallic means are generalizations of the golden ratio ($n=1$) and silver ratio ($n=2$), and share some of their interesting properties. The term "bronze ratio" ($n=3$), and terms using other metals names (such as copper or nickel), are occasionally used to name subsequent metallic means.

In terms of algebraic number theory, the metallic means are exactly the real quadratic integers that are greater than $1$ and have $-1$ as their norm.

The defining equation $x^{2}-nx-1=0$ of the nth metallic mean is the characteristic equation of a linear recurrence relation of the form $x_{k}=nx_{k-1}+x_{k-2}.$ It follows that, given such a recurrence the solution can be expressed as

$x_{k}=aS_{n}^{k}+b\left({\frac {-1}{S_{n}}}\right)^{k},$

where $S_{n}$ is the nth metallic mean, and a and b are constants depending only on $x_{0}$ and $x_{1}.$ Since the inverse of a metallic mean is less than 1, this formula implies that the quotient of two consecutive elements of such a sequence tends to the metallic mean, when k tends to the infinity.

For example, if $n=1,$ $S_{n}$ is the golden ratio. If $x_{0}=0$ and $x_{1}=1,$ the sequence is the Fibonacci sequence, and the above formula is Binet's formula. If $n=1,x_{0}=2,x_{1}=1$ one has the Lucas numbers. If $n=2,$ the metallic mean is called the silver ratio, and the elements of the sequence starting with $x_{0}=0$ and $x_{1}=1$ are called the Pell numbers.

Geometry

If one removes n largest possible squares from a rectangle with ratio length/width equal to the nth metallic mean, one gets a rectangle with the same ratio length/width (in the figures, n is the number of dotted lines).

Golden ratio within the pentagram (φ = red/ green = green/blue = blue/purple) and silver ratio within the octagon.

The defining equation ${\textstyle x=n+{\frac {1}{x}}}$ of the nth metallic mean induces the following geometrical interpretation.

Consider a rectangle such that the ratio of its length L to its width W is the nth metallic ratio. If one remove from this rectangle n squares of side length W, one gets a rectangle similar to the original rectangle; that is, a rectangle with the same ratio of the length to the width (see figures).

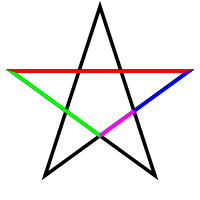
Some metallic means appear as segments in the figure formed by a regular polygon and its diagonals. This is in particular the case for the golden ratio and the pentagon, and for the silver ratio and the octagon; see figures.

Powers

Denoting by $S_{m}$ the metallic mean of m one has

$S_{m}^{n}=K_{n}S_{m}+K_{n-1},$

where the numbers $K_{n}$ are defined recursively by the initial conditions K₀ = 0 and K₁ = 1, and the recurrence relation

$K_{n}=mK_{n-1}+K_{n-2}.$

Proof: The equality is immediately true for $n=1.$ The recurrence relation implies $K_{2}=m,$ which makes the equality true for $k=2.$ Supposing the equality true up to $n-1,$ one has

${\begin{aligned}S_{m}^{n}&=mS_{m}^{n-1}+S_{m}^{n-2}&&{\text{(defining equation)}}\\&=m(K_{n-1}S_{n}+K_{n-2})+(K_{n-2}S_{m}+K_{n-3})&&{\text{(recurrence hypothesis)}}\\&=(mK_{n-1}+K_{n-2})S_{n}+(mK_{n-2}+K_{n-3})&&{\text{(regrouping)}}\\&=K_{n}S_{m}+K_{n-1}&&{\text{(recurrence on }}K_{n}).\end{aligned}}$

End of the proof.

One has also

$K_{n}={\frac {S_{m}^{n+1}-(m-S_{m})^{n+1}}{\sqrt {m^{2}+4}}}.$

The odd powers of a metallic mean are themselves metallic means. More precisely, if n is an odd natural number, then $S_{m}^{n}=S_{M_{n}},$ where $M_{n}$ is defined by the recurrence relation $M_{n}=mM_{n-1}+M_{n-2}$ and the initial conditions $M_{0}=2$ and $M_{1}=m.$

Proof: Let $a=S_{m}$ and $b=-1/S_{m}.$ The definition of metallic means implies that $a+b=m$ and $ab=-1.$ Let $M_{n}=a^{n}+b^{n}.$ Since $a^{n}b^{n}=(ab)^{n}=-1$ if n is odd, the power $a^{n}$ is a root of $x^{2}-M_{n}-1=0.$ So, it remains to prove that $M_{n}$ is an integer that satisfies the given recurrence relation. This results from the identity

${\begin{aligned}a^{n}+b^{n}&=(a+b)(a^{n-1}+b^{n-1})-ab(a^{n-2}+a^{n-2})\\&=m(a^{n-1}+b^{n-1})+(a^{n-2}+a^{n-2}).\end{aligned}}$

This completes the proof, given that the initial values are easy to verify.

In particular, one has

${\begin{aligned}S_{m}^{3}&=S_{m^{3}+3m}\\S_{m}^{5}&=S_{m^{5}+5m^{3}+5m}\\S_{m}^{7}&=S_{m^{7}+7m^{5}+14m^{3}+7m}\\S_{m}^{9}&=S_{m^{9}+9m^{7}+27m^{5}+30m^{3}+9m}\\S_{m}^{11}&=S_{m^{11}+11m^{9}+44m^{7}+77m^{5}+55m^{3}+11m}\end{aligned}}$

and, in general,

$S_{m}^{2n+1}=S_{M},$

where

$M=\sum _{k=0}^{n}{{2n+1} \over {2k+1}}{{n+k} \choose {2k}}m^{2k+1}.$

For even powers, things are more complicate. If n is a positive even integer then

${S_{m}^{n}-\left\lfloor S_{m}^{n}\right\rfloor }=1-S_{m}^{-n}.$

Additionally,

${1 \over {S_{m}^{4}-\left\lfloor S_{m}^{4}\right\rfloor }}+\left\lfloor S_{m}^{4}-1\right\rfloor =S_{\left(m^{4}+4m^{2}+1\right)}$

${1 \over {S_{m}^{6}-\left\lfloor S_{m}^{6}\right\rfloor }}+\left\lfloor S_{m}^{6}-1\right\rfloor =S_{\left(m^{6}+6m^{4}+9m^{2}+1\right)}.$

For the square of a metallic ratio we have:$S_{m}^{2}=[m{\sqrt {m^{2}+4}}+(m+2)]/2=(p+{\sqrt {p^{2}+4}})/2$

where $p=m{\sqrt {m^{2}+4}}$ lies strictly between $m^{2}+1$ and $m^{2}+2$. Therefore

$S_{m^{2}+1}<S_{m}^{2}<S_{m^{2}+2}$

Generalization

One may define the metallic mean $S_{-n}$ of a negative integer −n as the positive solution of the equation $x^{2}-(-n)x-1.$ The metallic mean of −n is the multiplicative inverse of the metallic mean of n:

$S_{-n}={\frac {1}{S_{n}}}.$

Another generalization consists of changing the defining equation from $x^{2}-nx-1=0$ to $x^{2}-nx-c=0$. If

$R={\frac {n\pm {\sqrt {n^{2}+4c}}}{2}},$

is any root of the equation, one has

$R-n={\frac {c}{R}}.$

The silver mean of m is also given by the integral

$S_{m}=\int _{0}^{m}{\left({x \over {2{\sqrt {x^{2}+4}}}}+{{m+2} \over {2m}}\right)}\,dx.$

Another form of the metallic mean is

${\frac {n+{\sqrt {n^{2}+4}}}{2}}=e^{\operatorname {arsinh(n/2)} }.$

Relation to half-angle cotangent

A tangent half-angle formula gives $$\cot \theta ={\frac {\cot ^{2}{\frac {\theta }{2}}-1}{2\cot {\frac {\theta }{2}}}}$$ which can be rewritten as $$\cot ^{2}{\frac {\theta }{2}}-(2\cot \theta )\cot {\frac {\theta }{2}}-1=0\,.$$ That is, for the positive value of ${\textstyle \cot {\frac {\theta }{2}}}$, the metallic mean $$S_{2\cot \theta }=\cot {\frac {\theta }{2}}\,,$$ which is especially meaningful when ${\textstyle 2\cot \theta }$ is a positive integer, as it is with some primitive Pythagorean triangles.

Relation to Pythagorean triples

Metallic Ratios in Primitive Pythagorean Triangles

Metallic means are precisely represented by some primitive Pythagorean triples, a² + b² = c², with positive integers a < b < c.

In a primitive Pythagorean triple, if the difference between hypotenuse c and longer leg b is 1, 2 or 8, such Pythagorean triple accurately represents one particular metallic mean. The cotangent of the quarter of smaller acute angle of such Pythagorean triangle equals the precise value of one particular metallic mean.

Consider a primitive Pythagorean triple (a, b, c) in which a < b < c and c − b ∈ {1, 2, 8}. Such Pythagorean triangle (a, b, c) yields the precise value of a particular metallic mean $S_{n}$ as follows :

$$S_{n}=\cot {\frac {\alpha }{4}}$$

where α is the smaller acute angle of the Pythagorean triangle and the metallic mean index is $n=2\cot {\frac {\alpha }{2}}={\frac {2a}{c-b}}=2{\sqrt {\frac {c+b}{c-b}}}\,.$

For example, the primitive Pythagorean triple 20-21-29 incorporates the 5th metallic mean. Cotangent of the quarter of smaller acute angle of the 20-21-29 Pythagorean triangle yields the precise value of the 5th metallic mean. Similarly, the Pythagorean triangle 3-4-5 represents the 6th metallic mean. Likewise, the Pythagorean triple 12-35-37 gives the 12th metallic mean, the Pythagorean triple 52-165-173 yields the 13th metallic mean, and so on.

Numerical values

First metallic means
N	Ratio	Value	Name
0	⁠0 + √4/2⁠	1
1	⁠1 + √5/2⁠	1.618033989	Golden
2	⁠2 + √8/2⁠	2.414213562	Silver
3	⁠3 + √13/2⁠	3.302775638	Bronze
4	⁠4 + √20/2⁠	4.236067978
5	⁠5 + √29/2⁠	5.192582404
6	⁠6 + √40/2⁠	6.162277660
7	⁠7 + √53/2⁠	7.140054945
8	⁠8 + √68/2⁠	8.123105626
9	⁠9 + √85/2⁠	9.109772229
10	⁠10+ √104/2⁠	10.099019513

See also

• Constant
• Mean
• Ratio
• Plastic ratio

Further reading

• Stakhov, Alekseĭ Petrovich (2009). The Mathematics of Harmony: From Euclid to Contemporary Mathematics and Computer Science, p. 228, 231. World Scientific. ISBN 9789812775832.

External links

• Cristina-Elena Hrețcanu and Mircea Crasmareanu (2013). "Metallic Structures on Riemannian Manifolds", Revista de la Unión Matemática Argentina.
• Rakočević, Miloje M. "Further Generalization of Golden Mean in Relation to Euler's 'Divine' Equation", Arxiv.org.