NOR gate

This article is about NOR in the sense of an electronic logic gate (e.g. CMOS 4001). For NOR in the purely logical sense, see Logical NOR. For other uses of NOR or Nor, see Nor (disambiguation).

"4001" redirects here. For the year, see 5th millennium. For the ROM for the Intel 4004 processor, see Intel 4001.

NOR gate truth table
Input		Output
A	B	A NOR B
0	0	1
0	1	0
1	0	0
1	1	0

The NOR gate is a digital logic gate that implements logical NOR - it behaves according to the truth table to the right. A HIGH output (1) results if both the inputs to the gate are LOW (0); if one or both input is HIGH (1), a LOW output (0) results. NOR is the result of the negation of the OR operator. It can also in some senses be seen as the inverse of an AND gate. NOR is a functionally complete operation—NOR gates can be combined to generate any other logical function. It shares this property with the NAND gate. By contrast, the OR operator is monotonic as it can only change LOW to HIGH but not vice versa.

In most, but not all, circuit implementations, the negation comes for free—including CMOS and TTL. In such logic families, OR is the more complicated operation; it may use a NOR followed by a NOT. A significant exception is some forms of the domino logic family.

Symbols

There are three symbols for NOR gates: the American (ANSI or 'military') symbol and the IEC ('European' or 'rectangular') symbol, as well as the deprecated DIN symbol. For more information see Logic Gate Symbols. The ANSI symbol for the NOR gate is a standard OR gate with an inversion bubble connected. The bubble indicates that the function of the or gate has been inverted.

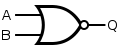
MIL/ANSI Symbol	IEC Symbol	DIN Symbol

NOR Full adder

Hardware description and pinout

NOR Gates are basic logic gates, and as such they are recognised in TTL and CMOS ICs. The standard, 4000 series, CMOS IC is the 4001, which includes four independent, two-input, NOR gates. The pinout diagram is as follows:

Pinout Diagram of a 4001 Quad NOR DIP-format IC

1 Input A1 2 Input B1 3 Output Q1 4 Output Q2 5 Input B2 6 Input A2 7 Vss 8 Input A3 9 Input B3 10 Output Q3 11 Output Q4 12 Input B4 13 Input A4 14 Vdd

Availability

These devices are available from most semiconductor manufacturers such as Fairchild Semiconductor, Philips or Texas Instruments. These are usually available in both through-hole DIP and SOIC format. Datasheets are readily available in most datasheet databases.

In the popular CMOS and TTL logic families, NOR gates with up to 8 inputs are available:

• CMOS
  • 4001: Quad 2-input NOR gate
  • 4025: Triple 3-input NOR gate
  • 4002: Dual 4-input NOR gate
  • 4078: Single 8-input NOR gate
• TTL
  • 7402: Quad 2-input NOR gate
  • 7427: Triple 3-input NOR gate
  • 7425: Dual 4-input NOR gate (with strobe, obsolete)
  • 74260: Dual 5-Input NOR Gate
  • 744078: Single 8-input NOR Gate

In the older RTL and ECL families, NOR gates were efficient and most commonly used.

Implementations

PMOS NOR gate with load resistor.

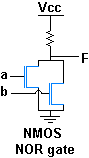The diagrams above show the construction of a 2-input NOR gate using NMOS logic circuitry. If either of the inputs is high, the corresponding N-channel MOSFET is turned on and the output is pulled low; otherwise the output is pulled high through the pull-up resistor.

The physical layout of a CMOS NOR

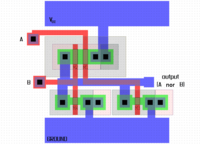
The diagram below shows a 2-input NOR gate using CMOS technology. The diodes and resistors on the inputs are to protect the CMOS components from damage due to electrostatic discharge (ESD) and play no part in the logical function of the circuit.

Unbuffered CMOS two input NOR gate

Functional completeness

Main article: NOR logic

The NOR gate has the property of functional completeness, which it shares with the NAND gate. That is, any other logic function (AND, OR, etc.) can be implemented using only NOR gates. An entire processor can be created using NOR gates alone. The original Apollo Guidance Computer used 4,100 integrated circuits (IC), each one containing only two 3-input NOR gates.

As NAND gates are also functionally complete, if no specific NOR gates are available, one can be made from NAND gates using NAND logic.

Desired gate	NAND Construction

See also

• AND gate
• OR gate
• NOT gate
• NAND gate
• XOR gate
• XNOR gate
• NAND logic
• Boolean algebra (logic)
• Flash memory